|
|
|
Никитин А.В.
-
1. Зачем всё это надо?
-
Зачеркнутая история Великих Идей 20 века.
И все же … снова – Разум?
Назад, к основам … — работа над ошибками.
-
Машинная жизнь.
Цель жизни.
Эволюция управления живых организмов.
Самостоятельность автоматических систем.
Внимание.
Образ.
Цель.
Выбор.
Связи.
Решения еще нет, а ответы – уже есть.
4. Счетная логика.
-
Причины и история появления счетной логики.
Понятия есть, но...
Основы для построения логического пространства.
Основания счетной логики.
Задачи, задачи…
-
Игры с числами.
Изображение элементов и их моделей.
Схемы логических элементов счетной логики.
Схемы узлов и счетчиков …
Литература:
5. Функциональные и электронные схемы.
Как давно это было…. С этого началось то, что потом стало называться — счетная логика. Все остальное было потом. Все построения, обоснования начинались вот с этого первого утверждения: Если число изменяется в результате счета в пространственной структуре, то оно представляет собой разрядные единицы, перемещающиеся в пространстве….
Было много удивления от простого понимания и осознания такого простого факта, что число – величина изменяемая, движущаяся…, в нем все время что-то меняется и куда-то убегает. То в одну сторону, то – в разные. Просто складывай единицы и смотри, что из этого получается. Конечно, я начал искать счетную систему, где эти процессы шли наиболее быстро. Оказалось, что все зависит от величины основания системы счета. И от …, и это было самым удивительным, иррациональности счетной системы. Рациональные системы сразу потеряли привлекательность. В них все было одномерным, медленным и скучным. Пока не нашлась удивительная единичная система. Она оказалась самой скоростной. Число вырастало быстро, но, что-то в ней было не так. Настоящее применение для единичной системы я нашел много позже, когда этот материал уже был опубликован в Интернете, а потом переделан множество раз.
От первоначального жонглирования числами мало что осталось. Слишком многое оказалось только красивым … пшиком. Детальный анализ множества красивых числовых конструкций показал их полную несостоятельность. Но, то что осталось, стало началом понимания, как и куда можно перемещать информацию по числу. Не теряя ее и не делая лишних движений. Здесь произвел вложение единицы в разряд числа, а получить ее можно уже где угодно, лишь бы число проходило через эту точку съема информации. Разрядная длина числа значения не имеет …
Такие каналы передачи сразу просто упирались в логическую систему. Не пойти дальше было уже просто невозможно. И, конечно, я пошел, а это оставил как… узелок — на память…
Узелок — на память.
Пространственная структура числа, полученная в той или иной системе счисления, уже не зависит от его количественного наполнения и линейного цифрового изображения.
Количество счетных единиц перестало однозначно определять изображение числа в пространственной форме представления.
А коли так, то можно использовать число в виде физической величины, не вдаваясь в его содержание. Как кирпичик, для строительства новых конструкций. Например, как линеечку или ниточку. И связать им что-нибудь – на память. Просто так, для интереса. И посмотреть, что получится. Я покажу это на примере, например, счета Бергмана.
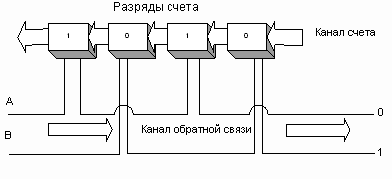
Рис.32. Счетная линейка Ф-счета.
В вычислительной технике счетный процесс проводится на счетных линейках, или счетчиках, реализующих счет в той или иной системе счисления. Счетная линейка, реализующая счет Бергмана, показана на рис.32.
Каждый разряд — триггер и необходимые логические элементы, обеспечивающие выполнение принципов счета Бергмана. Мы видим два канала движения счетных импульсов. Один – прямой канал счета и второй — канал обратной связи. Канал обратной связи имеет две ветви управления, которые объединяют четные и нечетные разряды счета, соответственно. Конечно, это только функциональная схема. Но она дает представление о технической реализации счета.
Все последующие построения предполагают их техническую реализацию на таких счетных линейках.
Для упрощения, в последующих схемах числовая цепь С01010101010С и будет означать такую счетную линейку. Пункты приема — схемы регистрации состояния разрядов счетчика. Пункты передачи – схемы передачи счетных импульсов на счетные входы соответствующих разрядов счета. Пункт трансляции – схема прямой трансляции, объединяет функции пунктов приема и передачи.
Но, сначала рассмотрим процесс переноса единицы. Для начала процесса переноса необходимо одно условие — разряды в направлении переноса должны быть заполнены. И разовое условие начала процесса переноса — операция сложения в нужном разряде. Как мы видим, в отличие от других систем счета, процесс переноса единицы может идти и влево, и вправо от разряда сложения. Максимальное заполнение разрядов в этой системе выглядит как …01010101010.… Начальные условия те же — заполненные разряды и наличие операции разрядного сложения.
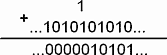 |
(78) |
Очень интересный результат. Слева, как и в других системах счета, движение единицы переноса оставляет после себя обнуленные разряды, а вот вправо единица переноса прошла, сдвигая заполненные разряды по числовой цепи, но оставила их полными и готовыми к следующему переносу. Отметим два обстоятельства. Мы добавляли единицу в заполненный разряд. И второе, при таком добавлении единицы возникает два процесса преобразования и две единицы переноса, движущиеся в разные стороны. Процессы возникают одновременно, но далее двигаются независимо друг от друга.
Возникает как бы два канала движения счетной единицы. Один канал счета — прямой, через который идет нормальный процесс счета, т.е. суммирования счетных единиц, а другой — обратный канал счета, который включается только при добавлении единицы в уже заполненный разряд. Он изменяет состояние младшего разряда, через один разряд справа от разряда суммирования. Таким образом, одновременно с нормальным движением единицы переноса влево, возникает и движение единицы переноса вправо от разряда сложения. Если в процессе правого переноса единица снова попадет в заполненный разряд, снова произойдет включение обратного канала счета с переносом единицы вправо. При заполненных разрядах счета такой перенос может быть достаточно продолжительным.
Добавлением единицы в заполненный разряд мы можем использовать правую часть числовой цепи как постоянно действующий канал передачи импульса преобразования. Мало того, мы можем на время отключить его. Попробуем действительно использовать числовую цепь как канал передачи.
Пунктом передачи у нас будут два самых старших, расположенных рядом разряда сложения. Они ограничивают разрядность числовой цепи, а в качестве пункта приема можно использовать любые два соседних разряда справа от разрядов сложения. Естественно, что единицы переноса, выходящие за пределы ограничения числовой цепи не влияют на ее состояние. Для поддержания канала передачи операцию сложения можно производить только с полным разрядом. Изменение состояния разрядов в пункте передачи проходят до пункта приема, и канал передачи поддерживается в проводящем состоянии. Схема (рис.33) содержит числовую цепь с ограничением сверху, двухразрядные пункт передачи и пункт приема.
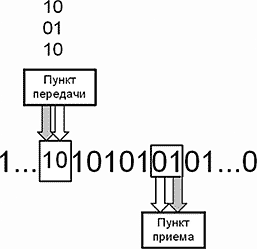
Рис.33. Дискретный канал передачи
Канал передачи информации получился не совсем обычный. Канал — дискретный, потому, что передает единицу от разряда к разряду, а не прямиком из пункта передачи на пункт приема. Его длина измеряется не метрами проводов, а количеством ячеек в канале связи. Он исправно передает единицы из пункта передачи в пункт приема, но по пути меняет состояние всех разрядов счета и в то же время не меняет состояние проводимости самого канала. По пути следования информации идет постоянная проверка работоспособности всех ячеек канала связи. При нарушении работоспособности какой-либо ячейки весь путь следования информации от этой ячейки до пункта передачи немедленно обнуляется, однозначно указывая место сбоя. Канал вполне может быть разветвленным. Ответвление канала может начинаться от любого разряда. Количество ответвлений ограничено только количеством ячеек дискретного канала передачи. Количество уровней ветвления также не ограничено. Мы получили кустовую проверочную сеть с одним пунктом управления. Один импульс с центра управления проводит проверку работоспособности всей разветвленной контрольной сети. Правда, не все так просто, но вполне возможно. Все хорошо, но жаль, что только в одном направлении. Нет контроля прохождения импульса по цепи. Можно использовать тот же дискретный канал для организации кольцевой системы проверки (Рис.34.). В этом случае, каждый уровень проверки представляет собой кольцевую схему. Пройдя весь путь, импульс проверки состояния возвращается в исходную точку и возвращает канал в исходное состояние. На один импульс управления канал ответит двумя циклами проверки. Связь уровней через пункт трансляции, также от любого разряда канала. К сожалению, связь центра и периферии, и в этом случае односторонняя. Но, можно сделать такую связь косвенным путем, используя выходы с обоих направлений каналов. Например, завести их в центр управления более высокого уровня. А дальше – дело техники.
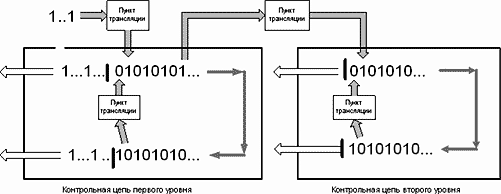
Рис.34. Многоуровневая система каналов контроля состояния.
Не правда ли, это очень напоминает нервную систему какого-то электронного организма? По крайней мере, все необходимое для этого есть. Может быть, в этом предназначение Ф-счета и счета Бергмана? Такое применение реализует большую часть их свойств и возможностей.
Связанные числа и числовые сети
Если расположить два числа таким образом, что один или несколько разрядов одного числа одновременно являются разрядами и второго числа, то такие числа можно назвать связанными числами, т.к. изменение одного числа в какой-то момент, автоматически ведет к изменению другого. Вот пример связанных чисел (Рис. 35.):
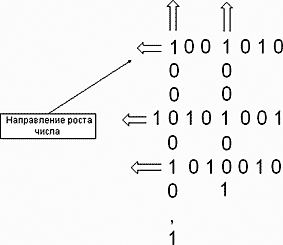
Рис.35. Пример связанных чисел
Естественно, что в реальном исполнении, на месте чисел располагаются счетные устройства, но для моделирования процессов нам вполне достаточно чисел. Связки чисел могут достигать больших размеров и сложности. Счет Бергмана предоставляет возможности построения сложных систем с различными видами связи и передачи изменения состояния счетных состояний из одного числа в другие. Такие системы связанных чисел и можно назвать числовыми сетями. На числовых сетях можно моделировать различные логические и счетные процессы.
Теперь моделируем генератор. Схема (рис.36.) включает две числовых цепи с ограничением сверху и два пункта трансляции. Нижняя числовая цепь имеет обратное направление счета. Если данные состояния контролируемых разрядов одной числовой цепи сразу передавать на разрядное суммирование в точке передачи другой числовой цепи, то это будет приводить к запуску процесса переноса в обеих цепях. Мы попадаем в режим циркуляции переноса единицы, как в числовых цепях, так и между ними.
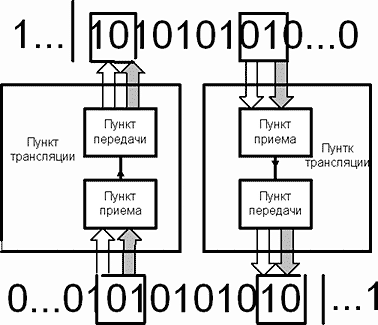
Рис.36. Генератор переноса единиц.
На этом можно остановиться. Вариантов использования любого варианта Ф-счета и счета Бергмана еще много. Но главное, я думаю, уже сказано. Это другой тип логики счета и поиска решений. Техническая реализация, даже показанных вариантов, уже приводит к новой архитектуре логических и счетных устройств. Логичное сочетание единичного, двоичного, счета Бергмана и, например, кодов Фибоначчи дает возможность реализовать новые свойства числа и обеспечить надежность хранения и передачи результатов достаточно простыми средствами. Область применения вполне определена.
***
Составление функциональной схемы логической задачи.
Если попытаться составить функциональную схему какой-либо логической задачи, то окажется, что стандартными средствами представления алгоритмов или электронными схемами это сделать затруднительно. Первые предназначены для нужд программирования, а вторые понятны только для специалистов. Вот здесь и возможно применение изображений элементов средствами счетной логики.
Изображение элементов и их моделей.
Вот элемент «И» и есть простейший RS триггер. Есть элементы и их взаимодействие. Так изображаются эти элементы, в принятом графическом оформлении. (Рис.37.):
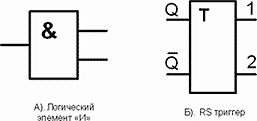
Рис.37. Элементы электронной логики.
Модификация изображения триггера показана на рис.38. Для средств моделирования полное изображение триггера не нужно. В процессе моделирования нам важна функция фиксации состояния принятого выхода этой электронной схемы. Все остальное на этом этапе можно не учитывать. Понятно, что для нормальной работы схемы нужны цепи начальной установки, обнуления и т.д. Но, в моделях они не учитываются, а только подразумеваются. Они будут, но потом, на этапе функциональной и электрической схемы…, а пока мы делаем лишь модель.
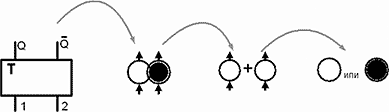
Рис.38. Модификация изображения RS триггера.
От триггера можно оставить только функцию фиксации. Это кружок черного (состояние 1) или белого (состояние 0) цвета. Это и есть состояние триггера для моделей. Движение единичного состояния в модели логической задачи показано стрелкой.
Так же проведем модификацию изображения элемента «И».
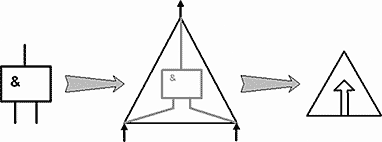
Рис.39. Модификация логического элемента «И».
Модификация логического элемента «И» показана на рис.39. Изменение изображения сделано из соображений подхода к элементу как детали конструктора для сборки различных моделей из одинаковых элементов. В этом элементе учтены основные возможные варианты сборки и геометрические особенности для моделирования.

Рис.40. Переход на моделирование средствами счетной логики.
Теперь покажем упрощение сборки в процессе моделирования. Мы все так же руководствуемся основной функцией каждого элемента. На рис.40. показана сборка из элементов «И» — вариант А), а также элементов «И» и триггеров, как элементов фиксации состояний в точках соединения — вариант Б).
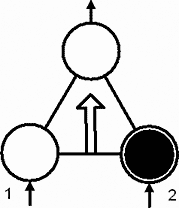
Рис.41. Базовая ячейка счетной логики
Я думаю, что рисунки объясняют примерные способы моделирования. Фиксируется состояние входов и выходов для схем совпадений. Выделим одну ячейку из показанных сборок моделей. Для полноты картины фиксирующие элементы есть на всех выводах.
На рис.41. показана ситуация, когда на входе 2 уже есть единичное состояние.
Выполнение операции «И» (Рис.42.) определяется появлением единичного состояния на выходе с обнулением триггеров входа. Они снова переходят в состояние 0. Все просто. Есть «1» на обоих входах – появляется «1» на выходе, а на входах – уже снова «0». Можно проводить новую счетную операцию.
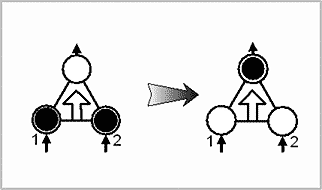
Рис.42. Выполнение счетной логической операции «И».
Отличие от простой логической операции очевидно. Счетные импульсы, поступающие на входы схемы совпадения, могут быть разнесены по времени. Идет последовательный набор состояний входов, необходимых для проведения операции «И».
Безусловно, элемент счетной логики с фиксацией состояний значительно сложнее простого логического элемента. Но и его возможности значительно шире.
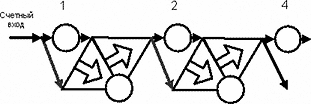
Рис.43. Пример построения двоичного счетчика средствами счетной логики.
Вот пример модели двоичного последовательного счетчика. (Рис.43.) Элементов фиксации состояния – триггеров, значительно больше, чем в классическом. На каждый разряд счета 2 триггера и еще 2 элемента «И». Но и считает такой счетчик несколько иначе, выполняя тот же двоичный счет.
Это только теоретическая модель. Но и она уже заставляет задуматься о том, что считать можно и иначе, чем принято сегодня, и вариантов много. В данном случае фиксируется каждый счетный импульс, отдельно, на своем триггере. Хорошо это или плохо – не знаю.
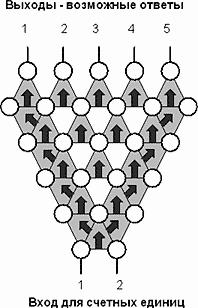
Рис.44. Пример логической задачи счетной логики.
Вот пример модели логической задачи. Схема (рис.44) имеет два входа для счетных импульсов. И пять выходов. Комбинацией импульсов на входе можно довести единичное состояние до любого выхода. Это пример достаточно сложного решения. Он приведен только из соображения симметричности построения и полной независимости выходов.
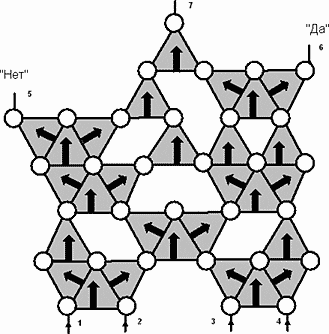
Рис. 45. Логическая структура на элементах счетной логики.
Вот еще один пример. Логическая структура (рис.45) отражает алгоритм решения логической задачи. До какого-то выхода мы доберемся в любом случае. Получить ответ – это не задача для такой логики. Важнее найти путь к планируемому ответу.
Какая комбинация счетных импульсов на входы структуры обеспечит продвижение и выход на нужный вариант ответа? И какая из правильных комбинаций самая оптимальная? Это и есть решение данной логической задачи.
Задача решается простыми вычислительными операциями, а ответ получается – логический.
Здесь показан только один вариант триггера и его включение в логическую цепь. И только в качестве фиксирующего элемента.
Функциональная схема логической задачи.
Теперь можно показать пример функциональной схемы логической задачи. Это тот же алгоритм, но он включает и много вариантные сетевые варианты соединения, чем напоминает и функциональную схему. Алгоритм предполагает условные и безусловные переходы, и один, пусть и извилистый путь решения задачи, и доведение его до результата. Мы пока не говорим о многофункциональном программировании, построенном на процедурах или модулях. Это уже не логическая задача, а исполнительная программа. Она не ищет решение, она его исполняет. Различие, согласитесь, существенное. Это другая задача и другое решение.
Схема, или карта решений показывает все возможности и пути, но не дает картинки решения. Под каждый путь свой алгоритм.
Я бы не заострял внимание на этом, если бы не одно «но» — все это делает человек. А должна делать – машина. На основе проб и ошибок в решении задачи.
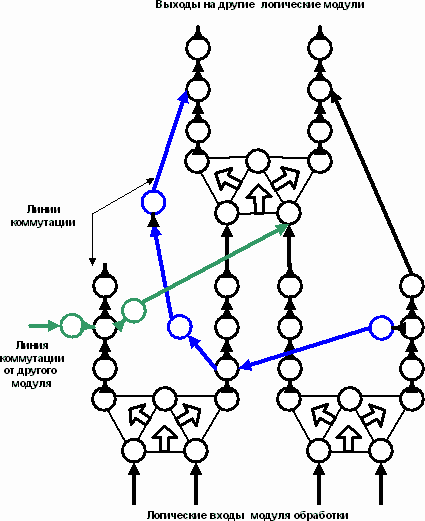
Рис. 46. Функциональная схема логического модуля в составе устройства.
Собирать, как элементы конструктора. Вот блок выбора, вот линия коммутации, а вот их соединение. Вот цель – точка перехода в другое пространство решения. Туда, только в эту точку необходимо привести числовую цепь, через имеющуюся уже структуру, или проложить новый канал, если есть из чего…, соединение и будет решением этой задачи. Новая задача – новый путь к новой точке выхода, … только пространство одно и то же. Постепенно оно заполняется линиями связей и узлами выбора путей. Задачи решаются и под каждую уже есть своя последовательность из 0 и 1 на входах модуля. Эта последовательность и есть — программа движения и действий в этом логическом пространстве на маршруте от входа до нужного выхода..
Для несостоявшихся решений необходимо искать другой логический модуль с другим начальным набором соединений логических элементов, или создавать новое…
Это только пример. Схема на рис.46. собрана только из двух элементов. Но, их же намного больше.
Схемы логических элементов счетной логики.
Применяемая сегодня электронная логика, по сути своей потенциальная. И хоть работает сегодняшний компьютер на огромных скоростях, логике импульс не нужен. Ей важно совпадение по времени. В импульсном режиме ее заставляют работать генераторы и счетчики этих самых импульсов. Через импульс логика становится хранителем времени.
Импульс вводит время в логику. Здесь начинается счет. Сколько импульсов, сколько длится передний фронт, сколько задний, скорость следования импульсов, скважность, и пр. и пр. Мгновения превращаются в микро…, нано… и пикосекунды. Быстрее, быстрее, еще быстрее. Изменение условий на входе должно сразу отражаться на выходе. Задержка отражения – неприятная необходимость.
А хотелось бы одновременности. Раз – и, раз – и все вместе, … вводим тактовую частоту, теперь еще раз. И так далее. Попали в такт – есть работа, не попали – извините, до свидания. Тактовая частота стала определять прогресс развития.
Все так. Но принцип остался потенциальный. Его лишь привязали ко времени. На жесткий поводок тактовой частоты.
Здесь можно вспомнить принцип эквивалентности:
Условия ![]() Эквивалент
Эквивалент ![]() Результат.
Результат.
В условиях жесткого тактирования результатом является попадание эквивалента в рабочий такт. Большего уже не требуется. Дополнительная фиксация результата уже вредна. Это дополнительная задержка во времени. Часто не оправданная. Зачем? Кончился рабочий такт, и кончились логические условия. Лучше решить задачу за один такт, чем фиксировать ее результат. Будет новый такт и новое решение.
Счетная логика, это логика импульса. Она выполняет принцип эквивалентности. Результат остается, даже если условия уже перестали действовать. Чтобы изменить результат надо ввести новые условия … и что-то с ними сделать.
По сравнению с существующей техникой это шаг назад. Обратно в «бестактность». В импульсы без строгого учета времени. В импульсы, как временные точки. У каждого свой отсчет.
Маленькие замечания:
- Понимание работы триггера самое древнее. Срабатывание происходит по переднему фронту импульса. И без учета его быстродействия. Есть импульс – есть переход в новое состояние. Если это возможно и соответствует его работе. Показанные схемы – функциональные.
- Появление единичного потенциала на входе 1 RS- триггера вызывает появление единичного потенциала на выходе Q, вне зависимости от его реального внутреннего устройства.
В начале разработки счетная логика базировалась на одном элементе – счетного «И». Но, реальность требует многообразия возможностей. Пришлось отказаться от простого решения. И ввести другие логические элементы…
Пока, все показанные логические схемы не привязаны к какой-либо счетной системе.
Пожалуй, только эту логическую операции математика оставила в том варианте, как этого требовала логика. К ответу ведет только определенное совпадение условий. В логике, это задача, противоположная счетному «ИЛИ». Единственность ответа при множественности и одновременности или последовательности действия заданных условий. Условий много, а ответ – один. В данном случае логическое умножение, как математическая интерпретация, выглядит убедительно. Логическое умножение не оговаривает последовательность, только одновременность, но … хоть так.
1![]() 1 =1 справедливо и для логической операции.
1 =1 справедливо и для логической операции.
На основе этой логической операции изначально и строилась концепция счетной логики.
Эту функцию мы уже неоднократно показывали. Она реализуется при условии выполнения начальной установки триггеров схемы рис.47.
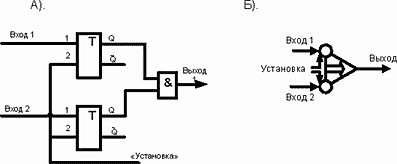
Рис.47. Счетное «И».
Вот эта схема и была показана ранее как основной элемент счетной логики. Счетная логика требует фиксации результата. Это достигается включением триггера на выходе 1, но это уже часть другого элемента. Потому он и не показан.
Логическая операция «ИЛИ» изначально, также имела другой смысл. Она означала, что любое решение задачи – правильное. Любое. Но, одно. Или это, или то, или вот это…
Одно начальное условие и множественность ответа.
Математика перекроила эту логическую посылку. И установила обратное ее понимание. Теперь наоборот, множественность возможных условий приводит к единственности ответа. И уже на этом основании ввела математическую интерпретацию. Логическое сложение.
1+1=1 мы же это помним.
Из задачи с множеством выходов нас привели к задаче с множеством входов. И закрепили это в логических электронных схемах.
Может быть, вернуться к начальному пониманию «ИЛИ»?
Управление выходами по входу. Ну, это совсем просто. Этой функции соответствует, например, триггер со счетным входом на рис.48.
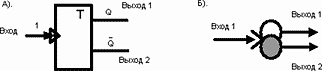
Рис. 48. Счетное «ИЛИ» выхода.
Любой новый импульс на счетном входе приведет к изменению состояния на выходах триггера. Уж, куда-нибудь он переключится…
Большее количество вариантов выбора, это увеличение количества выходов при единственности входа. Это уже управляемая коммутация.
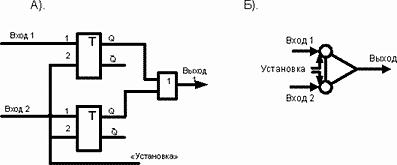
Рис.49. Счетное «ИЛИ» входа.
Функциональная схема счетного «ИЛИ» по входу приведена на рис.49. Она отличается от принятой логической схемы фиксацией единичного состояния входа. Если счетный импульс пришел на любой вход, то на выходе схемы он уже не пропадет. До переустановки схемы в исходное состояние.
Логическая операция «НЕ» основана на отрицании и исключении условия в ответе логической операции. В противопоставлении условия и ответа. «ДА» — «НЕТ». Одно условие и один результат. И результат противоположен условию.
0 – 1 и 1- 0, вот сегодняшняя математическая интерпретация такого противопоставления. Мы задаем условие и получаем его, вроде бы, противоположность. Как результат действия условия. Если «не черное», то – «белое»?
Не совсем так. «Не черное» — оно и есть, не черное. Какое угодно, только — не черное.
В математике логики есть только две цифры: 0 и 1.
Это привело к слиянию нескольких смыслов операции «НЕ» -,противоположности, противопоставления и исключения условия из результата. Вот и осталось одно противопоставление в виде противоположности. Да уж, иная простота – хуже воровства…
Далее математика определила свое дополнение: Нет условия и – нет результата.
Очень жесткое дополнение. И ограничение. Получается, что ответ в задаче есть, только пока мы решаем эту задачу. Решили, и — ответ пропал.
А мы так к нему стремились …
Но мы все же запишем ответ. И пусть все условия задачи пропадут, и уйдут из памяти, ответ, вот он – остался. Как результат операции. Это против математического ограничения, но соответствует философской концепции логики. Ответ в задаче должен быть. И если мы его нашли, то он должен остаться. Даже если задача уже не актуальна. Может быть, она для нас уже и не задача, мы же знаем ответ, но для следующих пытливых умов она снова встанет на пути. Знание ответа поможет им пойти дальше, чем довелось нам.
Вот на этом и остановимся. Математическое выражение противопоставления, это решаемая нами задача. И у задачи должен быть ответ, как результат её решения. Отдельно от выражения. Сам по себе. Уже, как событие для следующей задачи.
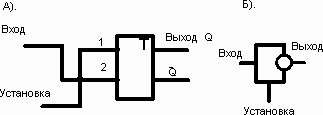
Рис.50. Счетное «НЕ».
В качестве элемента счетного «противоположного НЕ» можно использовать RS триггер. Только входы поменять местами, как на рис.50. Теперь подача импульса на вход приведет к появлению единичного состояния на выходе -Q. А на выходе Q появится состояние 0.
Что соответствует противоположности и противопоставлению логической функции НЕ:
| А |
(79) |
Результат в виде потенциала на выходе триггера останется и при прекращении действия условий на его входе. Это зафиксированный ответ логической задачи противопоставления.
Для изменения результата надо изменить условие на входе. В данном случае, подать импульс на другой вход — «Установка». И элемент снова готов к работе.
А как же смысл «НЕ» — исключение условия из результата операции?
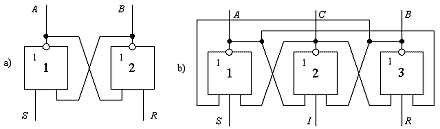
Рис.51. Триггеры на логических элементах.
Вот пример (рис.51. б) триггера на 3 устойчивых состояния. Он взят из публикаций А.П. Стахова [17 ].
Его работа соответствует смыслу «исключающего НЕ — ИЛИ» с фиксацией результата. Условие исключено, а на каком, из оставшихся выходов будет 1 – безразлично.
***
Вот они основные электронные логические элементы счетной логики. Наверное, возможны и другие по аналогии со схемами формальной электронной логики. Придет время, и они появятся. Жизнь не стоит на месте.
Счетная логика никак не отменяет принятую. Только дополняет.
Я не ставил себе цель полностью разобраться в архитектуре электронного аналога мозга. У меня для этого нет ни знаний, ни опыта, ни времени. Наверняка, современная наука давно предложила такую архитектуру и систему обработки информации.
Я лишь попробовал разобраться в устройстве предложенных мною элементов счетной логики. Составить возможную электронную схему элементов. Учесть связи, влияющие на их работу. Ввести возможность автоматического прогнозирования не на логическом, а на электронном уровне исполнения. На уровне схемного решения. То, что можно учесть в первом приближении. Я не силен в электронике, и мои решения, это только простейшие варианты реализации задуманного. В реальности все сложнее. Но начать можно и с малого, с азов…
Элемент выбора направления.
Элемент выбора направления, это коммутаторпозволяющий выбирать направление передачи входного импульса. Правое и левое. Это нулевой и два первых разряда разветвляющегося симметричного счетчика. Правое направление счета имеет продолжение на выходах С и E, а левое – на выходах С и D этого элемента. Управление и счет идет счетными импульсами, поступающими на входы А и В.
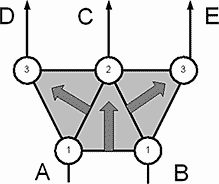
Рис.52. Элемент выбора направления.
На рис. 52. под треугольниками со стрелками скрываются логические элементы «И», а кружки – триггеры. Стрелки показывают направление счета в разряде. Такое обозначение элемента точно передает характер его работы и функциональную направленность. Функциональная схема элемента показана на рис.53. Она содержит пять триггеров и три логических элемента «И». Цепи обнуления не показаны. Рассказывая об основном элементе, я упомянул, что все триггеры находятся под двойным управлением. Вот теперь это можно рассмотреть чуть подробнее. Функционально, элемент выбора направления состоит из трех основных элементов. Но, это только формально. А в действительности?
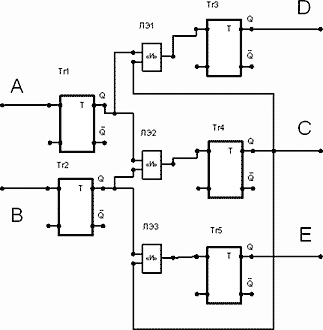
Рис.53. Схема элемента выбора направлений.
Основной элемент с входами А и В состоит из логического элемента «И» ЛЭ2, и трех триггеров – Тг1, Тг2, Тг4. Левый основной элемент с выходом D, это – логический элемент ЛЭ1 и триггеры Тг1, Тг4, Тг3. Правый основной элемент с выходом Е, это – логический элемент ЛЭ3 и триггеры Тг2, Тг4, Тг5. Таким образом, каждый триггер входит в состав двух основных элементов и, соответственно, ими и управляется.
Вводим моменты времени t=0, t=1, … и т.д. В эти моменты подаем счетные импульсы на входы А и В, и смотрим, что получится.
Данные сведены в таблице 4.
Таблица 4
|
t= |
А |
В |
Q1 |
Q2 |
C |
D |
E |
Примечание |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Исходное состояние |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
2* |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
Обнуление Тг1, Тг2. |
|
2 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
3* |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
Обнуление Тг1, Тг4. |
|
3 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
4 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
5* |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
Обнуление Тг1, Тг2. |
|
5 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
|
|
6 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
|
7* |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
Обнуление Тг1, Тг4. |
|
7 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
8 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
9* |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
Обнуление Тг1, Тг2, |
|
9 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
|
10 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
11 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Как мы видим, это нормальный счет в кодах Фибоначчи. Дальнейшая подача импульсов на входы элемента состояния уже не изменит. Для заполнения счетчиков достаточно комбинации из 10 счетных импульсов на входы А и В. Для выхода единичного состояния на выходы D или Е достаточно комбинации из трех счетных импульсов. Порядок следования импульсов можно записывать буквами входов. Например: А,В,А. И единичное состояние появится на выходе D. Для выхода Е, это – В,А,В. Выход С – А,В или В,А. Вот и весь выбор. Комбинация для полного заполнения счетчика, соответственно, А,В,А(это D), В,А,В(это Е), А,В(это С), А,В. И считайте в любую сторону. Собственно, здесь и начинается выбор. И стадия принятия решения. Куда? Вправо или влево?
Шаговое прогнозирование.
Счетная логика – логические связи с триггерным входом. Такая логика допускает лишь пошаговое выполнение логических операций. Это относительно медленная логика.
Введем в схему основного элемента дополнительную цепь, например, как на рис.54. Это цепь автоматического или технического прогнозирования. Контакт (2) соединяется с контактом (3) предыдущего элемента, а контакт (1) к внешнему управлению…
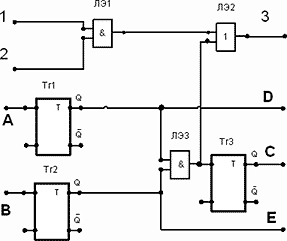
Рис.54. Основной логический элемент с цепями прогнозирования
Если на входе (1) есть разрешающий сигнал, то эта цепь получает все состояния счетной, но не может влиять на их исполнение. Посмотрим, как работает эта связка. Как только какой-либо элемент счетной логики начнет счетную операцию, так эти же единичные сигналы будут отработаны логической цепью прогнозирования. Ее отработка сводится к созданию логических единиц на всех каналах и выходах по линии взаимодействия. Нам надо зафиксировать зону влияния и состояние выходов. И отсечь лишнее. Полученная зона влияния и есть те возможные пути, по которым может продвигаться доминанта числа счетной логики. Мы получили прогнозирование по вариантам движения к ответу.
Показанный вариант самый простой, и вряд ли он способен работать реально. Видимо, действительно работоспособную схему надо еще разрабатывать. И она будет сложнее. Но и этот вариант позволяет правильно понять предлагаемые принципы прогнозирования в процессе решения.
Такая операция прогнозирования позволяет определять дальнейший путь к ответу. А в дальнейшем и корректировать этот путь, запоминая и отрабатывая только самый прямой. Запомнив этот путь можно вообще не двигаться по счетному пути. Он уже хорошо известен. Можно сразу перейти к нужному ответу, минуя этап поиска и движения. Перейти к шаблонам решений. Это резко сокращает время на решение задачи счетной логики. Теперь искать ответ и путь к нему надо только для новых логических задач.
Совмещение функций в схемах счетной логики.
Схемы, реализованные с рамках счетной логики давно известны специалистам по вычислительной технике и электронике. Под другими названиями и для реализации других практических задач. Видимо, вопрос только в том, под каким углом зрения смотрим мы на те или иные, давно известные схемы.

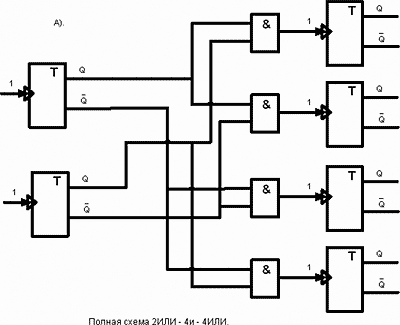
Рис.55. Полная схема 2ИЛИ -4и-4ИЛИ.
Вот пример такой схемы. Он на рис.55. Это логическая схема 2ИЛИ-4и-4ИЛИ.
Контроль повторения состояния входа.
Показанные на рис. 56. схемы реализуют изменение выхода при изменении состояния на входе.
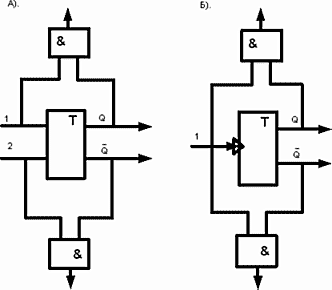
Рис.56. Контроль повторения состояния входа.
Как мы видим, схема показывает повторение состояния входа, при котором изменение состояния выхода уже не происходит.
Вариант А). может быть использован для фиксации появления состояний входов схемы 10+10=10. Вторичное появление единичного состояния на входе 1 никак не изменит состояния выхода Q, но это будет отражено на верхнем по схеме выходе логического элемента.
Вариант Б). отражает совпадение состояния входа и одного их выходов триггера.
Единичные состояния на выходах логических элементов позволяют ввести дополнительные варианты управления логическими цепями.
Коммутаторная линейка связи.
Линейка связи на рис.57. позволяет передать импульс от входа до выхода. И не только передать по самой линейке, но и отправить его по любой соседней такой же линии из точки соединения к выходу. Количество точек соединения зависит от длины линии связи. Длина измеряется ячейками передачи. Каждая ячейка включает RS- триггер и логику коммутации. В данном случае, это одна схема «И» и одна «ИЛИ». Ячейка имеет один вход и один выход для соединения с соседним каналами.
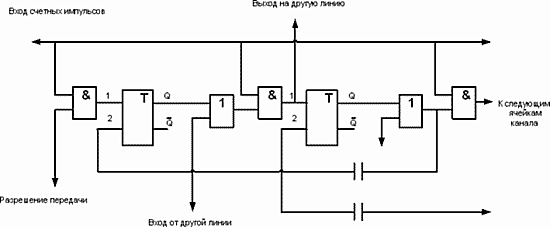
Рис.57. Коммутаторная линия передачи.
На основе такой линии связи возможно построение сложного коммутатора передачи импульсов. Сложность коммутатора ограничена только возрастанием сложности управления.
Счетчик импульсов единичного счета.
Это счетчик импульсов, работающий по законам единичного счета. Показано два разряда счета. Счетчик на рис. 58. позволяет делать как суммирование импульсов, так и вычитание. Для организации нужного режима работы необходимо подать единичный потенциал на соответствующий вход и обеспечить поступление счетных импульсов по соответствующему входу.
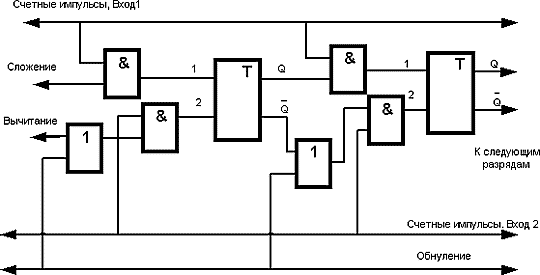
Рис.58. Счетчик единичного счета.
При наличии потенциала на шине «Обнуление» первый же счетный импульс на Вход 2 установит все ячейка счетчика в нулевое состояние.
Счетчик Ф-счета.
Счетчик импульсов, рис. 59.,на принципах Ф-счета позволяет реализовать счет по системе Бергмана и в кодах Фибоначчи. Это определяется схемой первой счетной ячейки. Особенности этих счетных систем усложнили схему, по сравнению со счетчиком двоичного счета, но это,… как посмотреть. Счетчик имеет входы для разрядного суммирования единиц. Но, надо соблюдать порядок суммирования. Это не параллельный сумматор…

Рис.59. Счетчик Ф-счета с независимыми разрядными входами для сложения разрядных единиц.
В запасе еще осталось несколько интересных и важных схем, но и приведенных вполне достаточно для демонстрации новых узлов логических устройств.
***
Никитин А.В. На пути к машинному разуму. Круг третий. (Часть 5) // «Академия Тринитаризма», М.,
|
|