Потенциальная и актуальная бесконечности

Таким образом, исследуя аксиомы непрерывности, лежащие в основе математической теории измерения, я вышел на «проблему бесконечности» — одну из важнейших проблем «философии математики». И разобраться в этой проблеме мне помогла книга Г.В. Чефранова «Бесконечность и интеллект», которая была написана на основе его докторской диссертации.

Прежде всего, следует отметить, что в математике нет единого определения понятия «бесконечность», хотя оно, как утверждает знаменитый немецкий математик Герман Вейль, лежит в основе математики. В процессе развития математики сформировались следующие подходы к этому понятию: арифметическая и геометрическая, потенциальная и актуальная бесконечности. Рассмотрим эти понятия подробнее.

Последовательность натурального ряда чисел

1, 2, 3, …,

(1)

представляет собой первый и самый важный пример бесконечного множества. Уже со времен Гегеля арифметическую бесконечность натурального ряда 1+1+1+ … в силу ее бесперспективности именуют «плохой» или «дурной» бесконечностью.

Геометрическая бесконечность состоит в неограниченном делении отрезка пополам. Паскаль писал по поводу геометрической бесконечности следующее: «Нет геометра, который бы не полагал, что пространство делимо до бесконечности. Без этого нельзя ему обойтись, как человеку нельзя быть без души. И тем не менее нет человека, который понимал бы бесконечную делимость …».

Кроме различия бесконечности натурального ряда и бесконечности геометрической, существует различие актуальной и потенциальной бесконечности. Для рассмотрения различий между этими понятиями вновь обратимся к натуральному ряду (1). Этот ряд можно рассматривать как «завершенный» ряд, заданный всеми своими членами одновременно. Такое представление о бесконечном называется актуальной бесконечностью.

Но натуральный ряд можно представить как ряд «развивающийся», «строящийся» по принципу n+1. Это означает, что каждое натуральное число может быть получено из предыдущего путем добавления к нему единицы. Такое представление о бесконечном называется потенциальной бесконечностью.

«Infinitum Actu Non Datur»

Как известно, математика превратилась в дедуктивную науку в Древней Греции. Уже в 6 в. до н.э. греческие философы разрабатывали проблему бесконечного и связанную с ней проблему непрерывного и дискретного. Большое внимание развитию этого понятия уделял Аристотель. Он был первым, кто категорически начал возражать против использования актуальной бесконечности в науке, ссылаясь на то, что, зная способы счета конечного числа объектов, нельзя эти способы распространять на бесконечные множества. Аристотелю принадлежит знаменитый тезис «Infinitum Actu Non Datur», что в переводе с латинского означает утверждение о невозможности существования логических или математических (т.е. всего лишь мыслимых, а не существующих в природе) актуально-бесконечных объектов. Большое влияние на развитие понятия бесконечности сыграли знаменитые «Апории Зенона», указывающие на логические трудности, связанные с гипотезой о бесконечной делимости отрезков пути и времени.

Рассмотрим только одну из них, называемую «Дихотомией». В этой апории Зенон утверждает, что движение невозможно, ибо до того, как движущееся тело пройдет расстояние от точки А до точки В, оно должно пройти , в затем этого расстояния. Но поскольку последовательность таких отрезков бесконечна, то это значит, что точка В никогда не будет достигнута. Парадокс (апория), выдвигаемый как непреодолимый логический тупик, состоит в том, что сумма бесконечного множества слагаемых конечна.

Теория бесконечных множеств Кантора

Немецкому математику Георгу Кантору (1845-1918) суждено было стать «возмутителем спокойствия» в математике 19-го века. Главным достижением Кантора стало создание теории бесконечных множеств. И главная его идея состояла в решительном отказе от Тезиса Аристотеля и рассмотрении бесконечных множеств, как актуально бесконечных множеств. В основу исследования бесконечных множеств Кантор положил идею взаимно однозначного соответствия элементов сравниваемых множеств. Если между элементами двух множеств можно установить такое соответствие, то говорят, что множества имеют одну и ту же мощность, то есть они являются равномощными или эквивалентными. «В случае конечных множеств, — писал Кантор, — мощность совпадает с количеством элементов». Вот почему мощность называют также кардинальным (количественным) числом данного множества. Указанный подход привел Кантора ко многим парадоксальным открытиям, резко противоречащим нашей интуиции. Так, в отличие от конечных множеств, на которые распространяется евклидова аксиома «Целое больше части», бесконечные множества этой аксиоме не подчиняются. Легко, например, установить равномощность множества натуральных чисел и его части – множества четных чисел путем установления следующего взаимно однозначного соответствия:

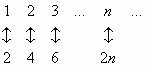
Эта характерная черта любого бесконечного множества может быть положена в основу его определения: множество называется бесконечным, если оно равномощно с одним из своих подмножеств. Конечным же называется множество, не эквивалентное ни одному из своих подмножеств. Любое множество, эквивалентное множеству натуральных чисел, называется счетным, так как его элементы можно занумеровать.

Еще более поразительным оказалось другое открытие, сделанное Кантором в 1873 г. Все три множества – натуральных чисел, рациональных чисел, алгебраических чисел – имеют одну и ту же мощность, иначе говоря, множество рациональных чисел и множество алгебраических чисел являются счетными множествами.

Кантор также доказал, что множество N натуральных чисел можно отобразить на часть множества R действительных чисел, но обратное утверждение не имеет места, то есть мощность действительных чисел больше мощности множества натуральных чисел.

До Кантора считалось, что прямая содержит меньше точек, чем плоскость. Однако в 1886 г. он доказал, что в единичном квадрате не больше точек, чем в единичном отрезке. Таким образом, мощность двумерного континуума оказалась равной мощности континуума одного измерения.

Уже из изложенного можно сделать вывод, что в отличие от большинства своих предшественников Кантор первый предпринял прямое и широкое исследование самой математической бесконечности, получив совершенно новые, неожиданные результаты.

То, что Кантор своей теорией множеств произвел революцию в математике, общеизвестно. Кульминационным пунктом в признании канторовской теории множеств можно считать конец 19-го века, когда математика приняла теорию множеств в качестве своей логической базы. Официальное провозглашение теоретико-множественных представлений фундаментом математики состоялось в 1897 г.: оно содержалось в речи Ж. Адамара на 1-м Международном конгрессе математиков в Цюрихе. В лекции подчеркивалось, что основная привлекательная причина теории множеств состоит в том, что впервые в истории математики была проведена классификация множеств на основе новоизобретенного понятия «мощности» и получены поразительные математические результаты, которые воодушевляли математиков на новые и удивительные открытия.

Обнаружение парадоксов в Канторовской теории множеств

Но не успели математики насладиться «математическим раем», предоставленным им Кантором своей теории бесконечных множеств, как спустя уже несколько лет после 1-го Международного конгресса математиков в теории множеств были обнаружены парадоксы или антиномии (от греческих слов «анти» — против и «номос» — закон), которые стали основой очередного, третьего по счету (после открытия несоизмеримых отрезков и обоснования теории пределов) кризиса в основаниях математики, который не преодолен и до настоящего времени.

Один из этих парадоксов был обнаружен знаменитым английским философом Расселом. Сам Рассел демонстрирует обнаруженный им парадокс на примере «деревенского парикмахера», который дал обещание брить всех тех и только тех жителей своей деревни, которые не бреются сами. Спрашивается: должен ли он брить самого себя? Если он будет брить себя, значит, он тем самым включает себя в число тех, которые бреются сами, и тогда он не должен брить себя; если же он не будет брить себя, то он уже будет принадлежать к тем, которые сами себя не бреют, и значит, он должен брить себя. Получается логическое противоречие, недопустимое в математике!

Как упоминалось, возникновение антиномий в теории множеств породило новый, третий по счету глубокий кризис основ математики. Были предприняты различные попытки преодоления этого кризиса. Наиболее радикальным из них является конструктивное направление в математике. Представители конструктивного анализа увидели основную причину парадоксов канторовской теории множеств в понятии «актуальной бесконечности». Наиболее убедительно критика в адрес этого понятия выражена в словах русского математика А.А. Маркова, одного из наиболее ярких представителей конструктивного анализа. Марков пишет:

«Мыслить себе бесконечный, т.е. никогда не завершаемый процесс как завершенный не удается без грубого насилия над разумом, отвергающим такие противоречивые фантазии».

Противоречие между аксиомами Евдокса-Архимеда и Кантора

Изучая аксиомы Евдокса-Архимеда и Кантора с точки зрения «актуальной» и «потенциальной» бесконечностей я обнаружил противоречие между ними. Ход моих рассуждений сводился к следующему. Анализ этих аксиом показывает, что аксиомы Евдокса-Архимеда и Кантора основаны на различных представлениях о бесконечном: аксиома Евдокса-Архимеда основана на использовании понятия «потенциальной» бесконечности, в то время как аксиома Кантора – на использовании понятия «актуальной» бесконечности, то есть между этими аксиомами, лежащими в основе теории действительных чисел, существует противоречие «актуальной» и «потенциальной» бесконечностей. Более того. Мне показалось, что, вводя свою аксиому, Кантор «слукавил». Действительно, в своей аксиоме он обращается к интуитивно ясному понятию «стягивающихся» отрезков, которое, в свою очередь, основывается на интуитивно ясном утверждении: «часть меньше целого» (каждый «стягивающийся» отрезок меньше предыдущего). Затем, с использованием своей аксиомы Кантор строит свою теорию бесконечных множеств, в которой он доказывает противоположное, то есть «часть равномощна к целому», что находится в противоречии с допущением о «стягивающихся» отрезков. Но если в основаниях теории действительных чисел (математическая теория измерения) заложены аксиомы, противоречащие друг другу, то и сама теория действительных чисел является противоречивой, что и выражается в современном кризисе в основаниях математики.

Переписка с А.Н. Колмогоровым

Я поделился своими рассуждениями с профессором Чефрановым, и он не нашел в них какого-либо изъяна. Он также посоветовал мне обратиться с этими идеями к одному из математических светил советской науки. И я написал об этом академику А.Н. Колмогорову. Колмогоров в своем ответе попытался опровергнуть мои рассуждения. Поскольку его ответ меня не удовлетворил, я попытался в одну из моих очередных поездок в Москву встретиться с академиком Колмогоровым. К сожалению, выдающийся математик встретил меня не очень приветливо, то есть серьезного разговора не получилось. Через несколько дней я понял, что причина этого была не во мне, а в той политической ситуации, в которой в тот момент находился Колмогоров. Именно в тот период был пик борьбы КПСС с «диссидентом» Андреем Сахаровым. ЦК КПСС вынуждало академиков подписать «осуждающее» письмо против академика Сахарова (и такое письмо, где была и подпись Колмогорова) было опубликовано. Однако попытка лишить Сахарова ученого звания академика (что решалось путем тайного голосования) не удалась: академики восстали против ЦК КПСС.

Мнение Игоря Витенько

После неудачного разговора с Колмогоровым я написал о своих идеях Игорю Витенько в Ужгород. Проблемы, поднятые мною, его весьма заинтересовали, и он прислал мне несколько весьма обстоятельных писем, в котором были изложены его взгляды на основания математики, в частности, теории чисел и теории измерения. В последнем из них он дал следующую оценку этим аксиомам:

«Из твоего письма я понял, что ты ударился в высокую философию. Между аксиомами Архимеда и Кантора я вижу только одно существенное (точнее принципиальное) различие: аксиома Архимеда — это конструктивная аксиома, т.е. для того, чтобы убедиться в справедливости соотношения nB>A нам нужно сделать только конечное (!) число шагов n. А аксиома Кантора — это не конструктивная аксиома. Для того, чтобы найти эту пресловутую среднюю точку, принадлежащую всем отрезкам, нужно сделать бесконечное число шагов. А последнее ни практически, ни теоретически не является возможным.

… Мне кажется, что аксиома Кантора как раз противоречит нашей житейской или физической интуиции.

Аксиома Кантора также (грубо говоря) эквивалентна утверждению, что для всякого объекта x можно сказать определенно обладает ли x неким свойством Р или нет. Но в действительности это не так. Такие свойства, как «быть кучей», «быть высоким человеком», «быть горячим предметом», «быть легким грузом», «быть горой». «быть лужей», «быть озером» не для всех предметов четко определены. Несомненно, 1 маковое зерно — не куча, а 10 тонн маковых зерен — это куча. Но постепенно (по маковому зерну), переходя от 1 макового зерна к 10 тоннам маковых зернам мы натолкнемся на такую совокупность маковых зерен, для которой трудно сказать куча это или не куча (т.е. для этой совокупности свойство быть кучей очень слабо определено или вообще не определено; с вероятностью 0,5 можно сказать, что это куча и с вероятностью 0,5 — что это не куча). Для таких свойств более естественной является трехзначная логика со значениями: истина, ложь и неопределенно. Один из моих аспирантов в своей диссертации разрабатывает эту логику.

Года два назад я интересовался парадоксами и пришел к выводу, что эти парадоксы (причем буквально все) разрешаются очень просто: есть такие предметы x и такие свойства Р, для которых с вероятностью 0,5 можно сказать, что x обладает свойством Р и с вероятностью 0,5 можно сказать, что x не обладает свойством Р. То есть все эти предметы (в определенном смысле) сводятся к парадоксу кучи. А в основе парадокса кучи лежит то, что мы требуем определенного ответа там, где его и быть не может.

Вывод: Аксиома Кантора — это очень абстрактная, далекая от действительности и практически не реализуемая модель физического мира. Эта пресловутая точка, что принадлежит всем отрезкам, это (выражаясь за Кантом) некая вещь в себе, которую мы полностью не охватим. Мне кажется, что отказ от аксиомы Кантора может дать большой эффект в прогрессе современной математики (и особенно вычислительной математики). Единственное, может быть, достоинство аксиомы Кантора состоит в том, что она нашему уму дает возможность на что-то опереться. То есть как-то приятно, что стягивание промежутков кончается точкой, т.е. что этот процесс стягивания имеет результат. Мы как-то более спокойно себя чувствуем, когда думаем, что при совершении бесконечного числа шагов измерения величины x мы получаем определенное действительное число. Хотя физика говорит, что измерять можно только до некоторых пределов (упомяну хотя бы принцип Гейзенберга).

Я не намерен отбрасывать аксиому Кантора. Пусть в чистой математике она властвует. Но прикладная математика, точнее, прикладной мат. анализ — я твердо убежден- должен развиваться без этой аксиомы.

С прикладной точки зрения, аксиома Кантора слишком мелочна и скрупулезна. При решении задач мы должны обращать внимание на более существенные вещи, а не на какую-то точку среди континуума равномощных ей точек.

То, что я высказал, я не хочу сказать, что это есть последнее слово науки; это мое мнение. Для более категорических заявлений нужны фундаментальные исследования в области математики и ее приложений».

Исследования Александра Зенкина

В 2002 г. после создания на Интернете моего сайта «Музей Гармонии и Золотого Сечения» мне прислал восторженное письмо известный русский математик Александр Зенкин. Когда я ознакомился с его исследованиями по проблеме бесконечного в математике, я понял, что именно он, возможно, поставит последнюю точку в споре с Кантором и в разрешении кризиса в современной математике. Суть подхода А. Зенкина, изложенного в ряде приоритетных публикаций, состоит в том, что он впервые четко сформулировал почти очевидный факт: концепция потенциальной бесконечности (ПБ) в Аристотелевой форме «все бесконечности суть потенциальны» и концепция актуальной бесконечности (АБ) в Канторовской форме «все бесконечные множества суть актуальны» являются АКСИОМАМИ, т.е. их нельзя ни доказать, ни опровергнуть, а только либо принять, либо отвергнуть. Именно поэтому все дискуссии о «существовании»/«не-существовании» АБ, ведущиеся со времен Аристотеля, никого ни в чем не убеждают. Здесь уместно провести некоторую аналогию с историей 5-го постулата Евклида о параллельных. Но есть и существенная разница: непротиворечивость не-евклидовых геометрий доказана, а непротиворечивость канторовской теории множеств, основанной на АКСИОМЕ АБ, — не доказана.

Проведя тщательный анализ Теоремы Кантора о несчетности континуума, в которой содержится «логическое» обоснование для правомерности использования АБ в математике, А. Зенкин приходит к следующему заключению:

1. Доказательство Кантора не является математическим доказательством в смысле Д.Гильберта и в смысле классической математики.

2. Вывод Кантора о несчетности множества Х «перепрыгивает» через потенциально бесконечный этап, т.е. рассуждение Кантора содержит фатальную логическую ошибку «недоказанного основания» («jump to a <wishful> conclusion»).

3. «Доказательство» Кантора, в действительности, доказывает, причем строго математически, именно потенциальный, т.е. принципиально незавершаемый, характер бесконечности множества Х «всех» действительных чисел, т.е. строго математически доказывает фундаментальный принцип классической логики и классической математики: «Infinitum Actu Non Datur» (Аристотель).

А дальше предоставим слово автору этого неординарного заключения:

«Ради исторической справедливости уместно добавить, что знаменитый Тезис Аристотеля «Infinitum Actu Non Datur», т.е. утверждение о невозможности существования (т.е. о внутренней противоречивости понятия) логических или математических (т.е. всего лишь мыслимых, а не существующих в природе) актуально-бесконечных объектов, — на протяжении последних 2300 лет, — разделяли и активно поддерживали такие великие единомышленники Аристотеля, как Лейбниц, Коши, Гаусс, Кронекер, Пуанкаре, Брауэр, Вейль, Лузин и многие другие выдающиеся создатели классической логики и современной классической математики в целом!

Каждый из них профессионально занимался исследованием проблемы математической бесконечности, и можно не сомневаться, что они понимали истинную природу Бесконечного отнюдь не хуже Г. Кантора. Особенно, если учесть тот принципиальной важности факт, что Бесконечность как таковая не зависит от прогресса и «технологической» оснащенности науки, поскольку никогда не была и никогда не станет объектом инструментального исследования — даже все мыслимые компьютеры, вместе взятые, никогда, по определению, не смогут завершить пересчет всех элементов натурального ряда чисел 1,2,3, … Именно поэтому все дискуссии о возможности или невозможности актуальной Бесконечности на протяжении двух тысячелетий и вплоть до Кантора носили чисто спекулятивный характер, не зависевший от очевидного (во всех других отношениях) прогресса науки. Только доказанная противоречивость следствий, вытекающих из понятия актуальной Бесконечности, могла стать «последним аргументом» против использования этого понятия в любой науке. Но для этого дискуссия об актуальной бесконечности должна была выйти за рамки спекулятивных рассуждений, основанных на чисто субъективных предпочтениях, в область аргументации, доступной для строгого логического анализа.

И в этом смысле, несомненная заслуга Г. Кантора состоит в том, что он первый от иногда более, иногда менее обоснованных рассуждений о возможности или невозможности актуальной бесконечности перешел к ее явному операциональному употреблению в рамках классической логики и классической математики, и тем самым впервые сделал результаты такого «математического» (см. выше) употребления понятия актуальной бесконечности доступными для стандартных методов логического и математического анализа. Именно такой анализ логических аспектов канторовского доказательства Теоремы о несчетности, — более, чем краеугольного камня всего канторовского «учения о трансфинитном», — выполненный выше, показывает, что основное допущение канторовского доказательства об актуальном характере бесконечности пересчета … ведет к нефинитному противоречию …, которое не имеет никакого отношения к методу Reduction ad Absurdum, а сама Теорема Кантора о несчетности является просто неверной с точки зрения классической логики (Аристотеля).

Почему такой анализ Теоремы Кантора не был выполнен своевременно, т.е. еще в конце 19-го века? — Это очень нетривиальная тема для фундаментального исследования в области психологии научного познания».

Таким образом, создается впечатление, что более чем 2,5-тысячелетняя история исследования понятия бесконечности как одного из фундаментального понятий математики близится к своему завершению. Антиномии канторовской теории множеств, вызвавшие современный кризис в основании математики, показали, что понятие актуальной бесконечности не может быть надежной основой для построения математики, так как это понятие, с точки зрения представителей конструктивного анализа, является внутренне противоречивым. С другой стороны, исследования современного русского математика Александра Зенкина свидетельствуют о наличии логических ошибок в доказательствах Георга Кантора, и это обстоятельство дает основание усомниться в истинности самой теории бесконечных множеств Кантора.

Таким образом, единственной прочной основой для построения математики остается введенное еще в греческой математике понятие потенциальной бесконечности; при этом тезис Аристотеля «Infinitum Actu Non Datur» и должен стать основной аксиомой для построения математики, лишенной противоречий!

Тезис Аристотеля другими словами выразил Давид Гильберт (известный своими «финитными» установками), который, рассуждая о конечном и бесконечном, пришел к следующему заключению:

«В заключение мы хотим из всех наших рассуждений сделать некоторое резюме о бесконечном – общий вывод таков: бесконечное нигде не реализуется. Его нет в природе, и оно недопустимо как основа нашего разумного мышления, — здесь мы имеем замечательную гармонию между бытием и мышлением».