Классические гиперболические функции

Из средней школы мы хорошо знаем тригонометрические функции, а именно синус, косинус и производные от них тангенс, котангенс и другие. Мы также знаем, что существует ряд математических соотношений, связывающих тригонометрические функции. Все, кто изучал тригонометрию, помнят об одном из них, связывающим косинус и синус:

cos2x +sin2x = 1.

(1)

Однако не все выпускники средней школы знают, что кроме тригонометрических синусов и косинусов существуют еще так называемые гиперболические функции, а именно гиперболический синус, гиперболический косинус и другие. Тригонометрические и гиперболические функции вместе с некоторыми другими важными математическими функциями образуют очень важный класс так называемых элементарных функций, которые очень широко используются в математике.

В отличие от тригонометрических функций, которые не имеют определения в аналитической форме, гиперболические функции могут быть представлены в следующем виде:

(2)

(3)

где число е – одна из важнейших математических констант математики (основание натуральных логарифмов).

Существует ряд изящных математических выражений для гиперболических функций. Одно из них, связывающих гиперболический синус и косинус, имеет следующий вид:

ch2x - sh2x = 1.

(4)

Гиперболические функции так же широко распространены в математике, как и тригонометрические функции. Наиболее известным примером их применения является неевклидова геометрия, созданная гениальным русским геометром Николаем Лобачевским в первой половине 19 в. Именно поэтому геометрию Лобачевского называется также гиперболической геометрией. В начале 20 в. известный немецкий математик Герман Минковский использовал гиперболические функции для весьма интересной геометрической интерпретации теории относительности Эйнштейна («четырехмерный мир Минковского»).

Николай Лобачевский (1792-1856) Герман Минковский (1864-1909)

Гиперболические функции Фибоначчи и Люка

Одним из современных математических результатов в теории чисел Фибоначчи, полученных представителями «Славянской «Золотой» Группы», является открытие так называемых гиперболических функций Фибоначчи и Люка. Расскажу об истории их открытия. Одним из внимательных читателей моей книги «Коды золотой пропорции» (1984 г.) был кандидат физико-математических наук Иван Семенович Ткаченко, которого я пригласил для работы на кафедре прикладной математики и вычислительных систем Винницкого политехнического института, организованной в 1989 г. (позже И.С. Ткаченко защитил докторскую диссертацию в области экономики). Однажды он взволнованно сообщил мне, что в результате изучения формул Бине, приведенных в моей книге «Коды золотой пропорции», он увидел их аналогию с гиперболическими функциями (2), (3) и что на этой основе может быть разработан новый класс гиперболических функций. Меня его идея заинтересовала и я активно подключился к ее развитию.

Для введения гиперболических функций Фибоначчи и Люка запишем эти знаменитые формулы, выведенные в 19 в. знаменитым французским математиком Бине, в следующем виде:

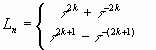(5)

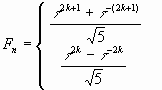(6)

где дискретная переменная k принимает значения из множества 0, ± 1, ± 2, ± 3, …

Заменим теперь дискретную переменную k в формулах (5) — (6) непрерывной переменной x, принимающей значения из множества действительных чисел, и для полученных таким путем четырех непрерывных функций переменной x введем следующие определения:

(1) Фибоначчиевый гиперболический синус

.

(7)

(2) Фибоначчиевый гиперболический косинус

.

(8)

(3) Люковый гиперболический синус

(9)

(4) Люковый гиперболический косинус

.

(10)

Заметим, что для дискретных значений переменной x=k фибоначчиевые и люковые гиперболические функции (7)-(10) совпадают с числами Фибоначчи и числами Люка, причем

sFk = F2k; cFk = F2k+1; sLk = L2k+1; cLk = L2k.

(11)

Свойство (11) является весьма характерной особенностью введенных выше гиперболических функций Фибоначчи и Люка по сравнению с классическими гиперболическими функциями (2), (3), которые однако не имеют «дискретного аналога».

Таким образом, основной результат, вытекающий из наших достаточно элементарных рассуждений, состоит во введении двух новых классов элементарных функций, класса фибоначчиевых гиперболических функций и класса люковых гиперболических функций. Эти функции очень похожи по своей форме на классические гиперболические функции, но отличаются от них одной особенностью. В отличие от классических гиперболических функций новые гиперболические функции имеют числовой аналог, а именно, числа Фибоначчи являются дискретным аналогом фибоначчиевых гиперболических функций, а числа Люка – дискретным аналогом люковых гиперболических функций. Именно этот факт является чрезвычайно важным для объяснения причин широкого проявления чисел Фибоначчи и Люка в живой природе (явление филлотаксиса).

«Непрерывный» подход к теории чисел Фибоначчи

Какое же значение имеют введенные выше гиперболические функции Фибоначчи и Люка для развития современной науки, в частности, математики? Чтобы ответить на этот вопрос, напомним, что для дискретных значений x=k (k=0, ± 1, ± 2, ± 3, …) фибоначчиевые и люковые синусы и косинусы совпадают с числами Фибоначчи и Люка, что задается соотношениями (11). Именно эти соотношения, связывающие числа Фибоначчи и Люка с гиперболическими функциями Фибоначчи и Люка, позволяют развить так называемый «непрерывный» подход к теории чисел Фибоначчи, которая является частью теории чисел, изучающей такие «дискретный объекты» как натуральные и целые числа. Тогда традиционный «дискретный» подход к теории чисел Фибоначчи может быть заменен «непрерывным» подходом, когда мы вначале находим некоторые тождества для гиперболических функций Фибоначчи и Люка, а затем даем им «фибоначчиевую» интерпретацию, используя (11).

Покажем плодотворность нового подхода к теории чисел Фибоначчи для того, чтобы установить еще одно важное тождество, связывающее фибоначчиевые функции (7), (8).

В теории чисел Фибоначчи известно следующее замечательное тождество, связывающее три соседних числа Фибоначчи:

.

(12)

Заметим, что тождество (12) справедливо для всех целых n (n=0, ± 1, ± 2, ± 3, …).

Мы можем, однако, записать тождество (12) в виде пары двух формул для четных n=2k и нечетных n=2k+1 значений дискретной переменной n:

;

(13)

.

(14)

Рассмотрим теперь формулы (13) и (14) с точки зрения гиперболических функций Фибоначчи. Используя (11), мы можем записать формулы (13), (14) в следующем виде:

;

(15)

,

(16)

где k=0, ± 1, ± 2, ± 3, ….

Однако, формулы (15), (16) можно рассматривать как частный случай следующих более общих утверждений:

.

(17)

.

(18)

Заметим, что формулы, связывающие между собой фибоначчиевые синусы и косинусы, в теории гиперболических функций Фибоначчи и Люка, по-видимому, играют ту же роль, что и хорошо известные нам формулы (1), (4), справедливые для тригонометрических и классических гиперболических функций. И эти формулы убеждают нас еще раз в том, что гиперболические функции Фибоначчи и Люка не есть выдумка Ткаченко и Стахова, а новый класс элементарных функций, отражающих некоторые глубокие математические закономерности окружающего нас мира.

Геометрия Боднара

Окончательно я поверил в гиперболические функции Фибоначчи и Люка после ознакомления с исследованиями львовского архитектора Олега Боднара по разработке новой геометрической модели филлотаксиса, изложенные в его книге «Золотое сечение и неевклидова геометрия в природе и искусства» (1994 г.). Независимо от нас с И.С. Ткаченко Олег Боднар ввел новый класс гиперболических функций, которые он назвал «золотыми» гиперболическими функциями. Именно такой подход позволил ему показать, почему на поверхности «филлотаксисных» форм в процессе их роста появляются числа Фибоначчи и Люка. С помощью такого подхода Боднар дал очень простое объяснения феномена роста «филлотаксисных» объектов. Однако внимательное ознакомление с «золотыми» гиперболическими функциями показало, что они отличаются от гиперболических функций Фибоначчи и Люка только постоянными коэффициентами. Это, однако, ни в коей мере не умаляет значения открытия Олега Боднара. Я многократно подчеркивал, что открытие львовского архитектора может быть сравнено с открытиями Кеплера или Ньютона. И не вина Боднара в том, что современная наука пока не в состоянии оценить его выдающееся открытие. А разве по-другому было с открытием Николая Лобачевского или Эвариста Галуа в 19 веке? Ведь было время, когда теория «казанского ректора» Лобачевского было предметом насмешек в российской академической науке, а гениальные математические работы Галуа французские академики-математики выбрасывали в мусорную корзину. Я уверен, что наступит время, когда открытие Боднара будет внесено в реестр выдающихся открытий 20-го века.