Новый класс иррациональных чисел

Сразу же после защиты докторской диссертации я ввел в рассмотрение еще одно важное понятие, так называемые «обобщенные золотые сечения» или «золотые р-сечения». При этом я рассуждал следующим образом. Если взять отношение соседних чисел Фибоначчи F_n/F_n-1 , то предел этого отношения стремится к золотой пропорции.

А теперь рассмотрим отношение соседних p-чисел Фибоначчи и исследуем, чему равен предел этого отношения при n ® Ґ. С этой целью обозначим искомый предел через x, то есть:

.

(1)

Представим теперь отношение соседних p-чисел Фибоначчи в следующем виде:

(2)

Принимая во внимание обозначение (1) для n ® Ґ можно заменить выражение (2) следующим алгебраическим уравнением:

xp+1 = xp + 1.

(3)

Обозначим через t _p действительный корень алгебраического уравнения (3). Исследуем теперь уравнение (3) для различных значений p. Для p = 0 уравнение (3) вырождается в тривиальное уравнение x = 2. Для p = 1 уравнение (3) сводится к алгебраическому уравнению золотой пропорции:

x2 = x + 1

(4)

которое имеет действительный корень .

Таким образом, уравнение (3) можно рассматривать как некоторое обобщение уравнения золотой пропорции (4). При этом уравнение имеет следующую «естественную» геометрическую интерпретацию. Разделим Отрезок AВ точкой C в следующем отношении:

,

(5)

где p = 0, 1, 2, 3, ... .

Заметим, что пропорция (5) сводится к дихотомии для случая p=0 и к классическому золотому сечению для случая p = 1. Учитывая это обстоятельство, деление отрезка AB точкой C в отношении (5) я назвал золотым p-сечением, а реальный корень уравнения (3) золотой p-пропорцией.

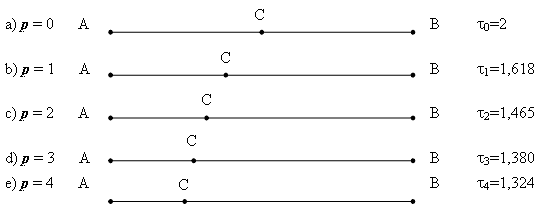
Золотые p-сечения (p = 0, 1, 2, 3, ...)

Легко показать, что из алгебраического уравнения (3) непосредственно вытекает следующее свойство золотой p-пропорции:

.

(6)

Для n=1 тождество (6) принимает следующую форму:

.

(7)

Запишем теперь тождество (7) в следующей форме:

.

(8)

Из (8) вытекает, что золотая p-пропорция преобразуется в число, инверсное p-й степени золотой p-пропорции при вычитании из нее 1.

Заметим, что для случая p = 0 мы имеем t _p = 2 и тождество (6) сводится к следующему тривиальному тождеству для двоичных чисел:

2ⁿ = 2^n-1 + 2^n-1 .

Для p = 1 мы имеем t _p = t = и тождество (6) сводится к следующему:

Таким образом, в результате исследования отношения соседних р-чисел Фибоначчи я получил ряд достаточно интересных результатов в теории чисел Фибоначчи и «золотого сечения». Самое главное, что мне удалось обобщить задачу о золотом сечении и ввести новое математическое понятие «золотых р-сечений», частным случаем которых является «дихотомия» (р=0) и классическое золотое сечение (р=1). И введенный мною новый класс иррациональных чисел широко используется в современной научной литературе.

Однако наиболее неожиданным явилось использование чисел Фибоначчи в так называемом «законе структурной гармонии систем», открытым недавно белорусским философом Эдуардом Сороко.

Закон структурной гармонии систем

Суть рассуждений Эдуарда Сороко состоит в следующем. Как известно, с философской точки зрения всякий объект природы, всякая система могут быть представлены как диалектическое единство двух противоположностей A и B. Это диалектическая связь может быть выражена в следующем виде:

A + B = U (universum).

(9)

Равенство (9) является наиболее общей формой выражения так называемого закона сохранения.

Здесь А и В различия внутри единства, логически непересекающиеся классы или состояния субстрата некоторого целого. Единственное условие: А и В должны измеряться одной и той же мерой, быть членами отношения, лежащего внутри единства.

Примерами (9) могут быть вероятность и невероятность событий, масса и энергия, ядро атома и его оболочка, вещество и поле, анод и катод, животные и растения, духовное и материальное начала в системе ценностей, доход и расход и т.д.

Частным случаем (9) является «закон сохранения информации»:

I + H = log N

(10)

где I – количество информации и H – энтропия системы, имеющей N состояний.

В процессе самоорганизации любая система переходит в некоторое стабильное состояние, называемое состоянием «термодинамического равновесия». И тогда возникает вопрос: в какой пропорции должны находиться стороны A и B диалектического противоречия (9) в состоянии термодинамического равновесия? Ответ на этот вопрос содержится в «законе структурной гармонии систем», сформулированном Эдуардом Сороко:

«Обобщенные золотые сечения суть инварианты, на основе и посредством которых в процессе самоорганизации естественные системы обретают гармоничное строение, стационарный режим существования, стуктурно-функциональную …устойчивость».

Эдуард Сороко приводит в своей книге «Структурная гармония систем» огромное количество примеров из различных областей природы, науки, и искусства, демонстрирующих действие своего закона. Ясно, что практическое использование «закона структурной гармонии систем» может принести существенный выигрыш при решении многих технологических, экономических, экологических и других задач, в частности, для совершенствования технологий изготовления структурно-сложных продуктов, контроля биосферы и т.д.

В чем же принципиальная особенность «Закона Сороко»? Начиная с Пифагора, ученые связывали понятие математической гармонии с единственной золотой пропорцией . «Закон Сороко» утверждает, что гармоничное состояние системы, соответствующее классической золотой пропорции, не является единственным и что для одной и той же системы может существовать бесконечное количество «гармоничных» состояний, соответствующих числам t _p, которые являются корнями алгебраического уравнения (3) и выражают некоторые неизвестные ранее свойства треугольника Паскаля.

Когда в 1984 г. была опубликована книга Эдуарда Сороко, мне было очень приятно, что Эдуард Максимович отметил мой вклад в развитие этого важного научного направления. На с. 201 своей книги он написал: «Открытие обобщенных чисел Фибоначчи насчитывает каких-нибудь полтора-два десятка лет. Сразу же было осознано, что s-числа непосредственно связаны с принципиально новым подходом к проблеме оптимизации систем. «Одним из неожиданных результатов теории оптимальных алгоритмов измерения, пишет А.П. Стахов, одним из первых начавший работать в этой области, — являются «фибоначчиевые» алгоритмы … в которых обобщенные числа Фибоначчи представляют собой длины эталонных отрезков измерения». Можно поэтому предположить, что распространенный в природе естественный процесс квантования должен иметь в своей сущности принцип действия фибоначчиевых алгоритмов как наиболее простой из возможных».