Числа Фибоначчи и Люка связаны с золотой пропорцией с помощью удивительных математических формул, которые были выведены в 19-м столетии французским математиком Бине, о котором будет рассказано ниже.

И подобно тому, как имя Фибоначчи связано с числами Фибоначчи, имя Бине в современной науке ассоциируется с замечательной математическими формулами, устанавливающими связь чисел Фибоначчи и Люка с «золотой пропорцией».

Для вывода «формул Бине» рассмотрим выражения для нулевой, первой и минус-первой степеней золотой пропорции:

t ⁰ = 1, t ¹ = , и t ^-1 = .

Вспомним теперь, что степени золотой пропорции связаны друг с другом следующим тождеством:

t n = t n-1 + t n-2.

(1)

Используя тождество (1), мы можем представить вторую, третью, четвертую степени золотой пропорции в «явной форме»:

t ² = t ¹ + t ⁰ = ;

t ³ = t ² + t ¹ = ;

t ⁴ = t ³ + t ² = .

Можно ли усмотреть в этих формулах какую-то закономерность? Прежде всего, заметим, что каждое выражение для степени золотой пропорции имеет одну и ту же форму:

.

Что же собой представляют числовые последовательности А и В в этих формулах? Нетрудно убедиться, что ряд чисел А представляет собой последовательность чисел 1, 3, 4, 7, …, а ряд чисел В представляет собой последовательность чисел 1, 1, 2, 3, …. Но первая последовательность представляет собой числа Люка, а вторая – числа Фибоначчи! Из этих примеров мы можем догадаться, что в общем виде формула, которая позволяет представить любую (n-ю) степень «золотой пропорции» с использованием числа Люка L_n и числа Фибоначчи F_n должна иметь следующий вид (и это, действительно, было доказано Бине еще в 19-м веке):

.

(2)

Заметим, что формула (2) справедлива для любого целого n.

Используя формулу (2), можно также очень просто выразить числа Люка L_n и числа Фибоначчи F_n через «золотую пропорцию». Для этого достаточно, используя (2), представить сумму или разность следующих степеней «золотой пропорции» t ⁿ + t ^-n и t ⁿ — t ^-n:

t n + t -n = ;

(3)

t n — t -n = .

(4)

Рассмотрим теперь, во что вырождаются формулы (3) и (4) для четных значений числа n = 2k. Для этого вспомним одно чудесное свойство чисел Фибоначчи: для четных значений n числа Фибоначчи F_2kи F_-2k равны по абсолютной величине, но противоположны по знаку, то есть F_-2k = — F_2k, а числа Люка L_2kи L_-2k для этого случая совпадают, то есть L_-2k= L_2k. Тогда для этого случая формулы (3), (4) принимают следующий вид:

t 2k + t -2k = L2k;

(5)

t 2k - t -2k = F2k.

(6)

Для нечетных значений n = 2k+1 имеют место следующие соотношения для чисел Фибоначчи и Люка: F_-2k-1 = F_2k и L_-2k-1 = L_2k+1. Тогда для этого случая формулы (5), (6) сводятся к следующему:

t 2k+1 + t -(2k+1) = F2k+1;

(7)

t 2k+1 — t -(2k+1) = L2k+1.

(8)

Следующие замечательные выражения для чисел Люка и Фибоначчи вытекают непосредственно из формул (5)-(8):

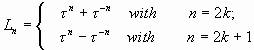(9)

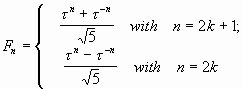(10)

Анализ формул (9), (10) дает нам возможность ощутить истинное «эстетическое наслаждение» и еще раз убедиться в мощи человеческого разума. Действительно, ведь мы знаем, что числа Фибоначчи и числа Люка всегда являются целыми числами. С другой стороны, любая степень «золотой пропорции» является иррациональным числом. Отсюда вытекает, что целые числа L_n и F_n с помощью формул (9), (10) выражаются через специальные иррациональные числа.

Например, число Люка 3 (n=2) согласно (9) может быть представлено как

,

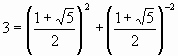(11)

а число Фибоначчи 5 (n=5) как

.

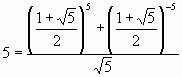(12)

Для того, чтобы убедиться в справедливости выражения (11) достаточно вспомнить, что согласно (2) имеют место следующие представления:

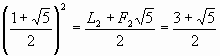и .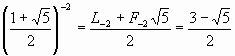

Если теперь подставить эти выражения в (11), то получим, что левая часть тождества (11) равняется ее правой части.

Для того, чтобы убедиться в справедливости выражения (12), достаточно вспомнить, что согласно (2) имеют место следующие представления:

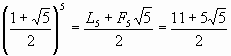и .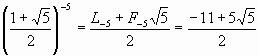

Если теперь подставить эти выражения в (12), то получим следующее выражение для правой части (12):

,

откуда вытекает справедливость тождества (12).

Из этих рассуждений мы видим, что формулы Бине затрагивают некоторые глубокие теоретико-числовые проблемы, находящиеся на стыке целых (числа Фибоначчи и Люка) и иррациональных чисел («золотая пропорция»).

Таким образом, начав наши «вариации» с чисел Фибоначчи, мы затронули множество интересных вопросов, относящихся к алгебре и теории чисел. Разумеется, эти «вариации» далеко не исчерпывают все удивительные свойства чисел Фибоначчи. Однако даже рассмотренных примеров достаточно, чтобы понять простую истину: подобно тому, как незатейливая мелодия таит в себе несравненно больше, чем кажется при первом прослушивании, простая математическая задача «о размножении кроликов» при всестороннем рассмотрении позволяет заглянуть в широкий круг актуальных проблем современной математики.