Равнобедренный треугольник

Раскрывая суть математического моделирования структур гармоничного мироустройства космического бытия, Платон называет две всеобщие элементарные модели, порождающие круговое движение и порождаемые круговым движением. «Итак, нам приходится отдать предпочтение двум треугольникам, как таким, из которых составлено тело огня и (трех) прочих тел: один из них равнобедренный, а другой таков, что в нем квадрат большей стороны в три раза больше квадрата меньшей» [1]. Далее, зная теорему Пифагора, не трудно догадаться, что второй треугольник – прямоугольный.

Таким образом, по Платону, изНАЧАЛьной (всеобщей элементарной) геометрической «порождающей моделью» гармонии космического бытия является равнобедренный треугольник. Посмотрим, как это ключевое положение Платона об элементарных началах бытия нашло свое отражение и развитие в элементарных началах геометрии средней школы [2], в «Главе II. Треугольники» (С. 27-51).

В данной главе почему-то не дается классификация треугольников. Она приводится только в IV главе «Соотношения между сторонами и углами треугольника». В этой главе рассматриваются остроугольные, тупоугольные и прямоугольные треугольники и соотношения между их сторонами и углами. Их гармоничная связь с равнобедренным треугольником не рассматривается. В Учебнике опубликовано «Практическое задание» №104 к главе II: «Начертите три равнобедренных треугольника так, чтобы угол, лежащий против основания, был а) острым; б) прямым; в) тупым». Разумеется, задание не предполагает выяснить какую-либо связь между начерченными раздельно треугольниками, поскольку учащиеся еще ничего не знают о теореме Пифагора и ее следствиях.

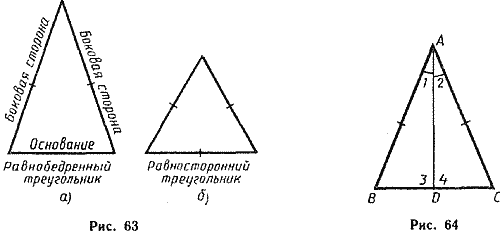
Ниже, я прилагаю из учебника полную сканеркопию обязательных знаний для гражданина со средним образованием и для потенциального студента о равнобедренном треугольнике, изложенных на с.34-35.

Разумеется, в школьной программе элементарные знания о треугольниках вообще, и о равнобедренном треугольнике, в частности, и их свойствах даны не полно и я, ниже, попытаюсь их восполнить.

Аксиома. Высота любого треугольника, опущенная с любой вершины на противоположную ей сторону, всегда делит треугольник на два прямоугольных треугольника.

Т е о р е м а. Медиана равнобедренного треугольника делит треугольник на два равных и симметричных прямоугольных треугольника.

Д о к а з а т е л с т в о. Рассмотрим треугольники ABD и ACD (рис.64). Медиана AD является высотой треугольника АВС и общей стороной треугольников ABD и ACD. и образует вместе с основанием два прямых (равных) угла: и делит его на два равных отрезка. То есть сторона BD = CD. Таким образом, треугольники ABD и ACD являются прямоугольными.

В согласии с теоремой: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Теорема доказана.

Одним из фундаментальных обобщений символических (математических) логик является разложение противоположных сущностей на двухэлементное множество. Данное положение можно отразить не только посредством символов арифметики и алгебры, но и – геометрически. Продолжим нашу тему «Сакральные треугольники…» и последовательную нумерацию рисунков к ней.

Равнобедренные треугольники, по углу, образуемому боковыми сторонами и имеющими одно основание (Рис.4), могут быть: равносторонними, остроугольными, тупоугольными и прямоугольными. Данная типизация равнобедренных треугольников, имеющих одно основание, в школьной программе обучения и учебниках отсутствует.

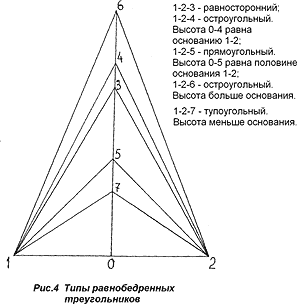
Почему Платон «отдает предпочтение» равнобедренному треугольнику, а не равностороннему? Потому, что равнобедренный треугольник по своим геометрическим параметрам и функциональным свойствам много богаче равностороннего. Подобно тому, как круг является частным случаем эллипса, квадрат – частным случаем прямоугольника, так и равносторонний треугольник является частным случаем равнобедренного треугольника. Только у него боковые стороны равны основанию.

Частным случаем равнобедренного треугольника является так же прямоугольный равнобедренный треугольник. Он единственный из всего многообразия равнобедренных треугольников, у которого боковые стороны образуют прямой угол, а высота равна половине основания. Прямоугольный равнобедренный треугольник, как и равносторонний, может бесконечно делиться и умножаться на себя подобные, прямоугольные равнобедренные треугольники.

Частным случаем равнобедренного треугольника является так же треугольник, у которого высота равна основанию. По большому счету, любой, из бесконечного множества равнобедренных треугольников, являет собой частный случай. Почему же нас интересуют в первую очередь прямоугольный равнобедренный треугольник и равнобедренный треугольник, у которого высота равна основанию? Потому, что если принять за единицу («1») общей меры длину стороны равностороннего треугольника бесконечного множества равнобедренных треугольников, то мы получаем возможность построения бесконечного множества равнобедренных треугольников на одном основании и симметрично равных прямоугольников. Мы получаем возможность относительного вычисления длин сторон треугольников и их площадей одной мерой, мерой основания. Так, в треугольнике 1-2-5 угол 152 – прямой. Основание 1-2 = 1; катеты прямоугольного треугольника 0-1-5 равны. 0-1 = 0-5 = 0,5.

А к с и о м а. Высота равнобедренного прямоугольного треугольника, опущенная с прямого угла на гипотенузу, делит («рассекает») гипотенузу и площадь треугольника на два равных, симметрично расположенных, равнобедренных прямоугольных треугольника.

1. Боковая сторона 1-5 равнобедренного треугольника 1-2-5 (Рис.4) является гипотенузой прямоугольного треугольника 0-1-5 у которого катеты равны и вычисляется в согласии с теоремой Пифагора:

   

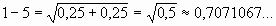
   Следствие (Рис.5): Гипотенуза 1-3 равнобедренного прямоугольного треугольника, боковая сторона которого равна«1», равна 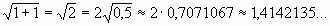То есть длина стороны, вписанного в окружность квадрата, равна ≈ 1,4142135 длины ее радиуса.
   

2. Боковая сторона 1-4 треугольника 1-2-4, является гипотенузой прямоугольного треугольника 0-1-4, у которого катет 0-4 равен 1, вычисляется аналогично и равна:

   

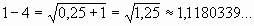
3. Высота равностороннего треугольника 1-2-3… 0-3 ≈ 0,8660254…

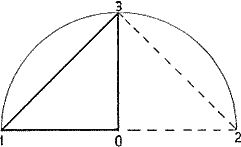Рис. 5. Вписанные, в четверть и в половину окружности равнобедренные прямоугольные треугольники

Возможности вычисления параметров равнобедренных и прямоугольных треугольников значительно возрастают, если их единая мера совпадает по величине с единой мерой круга, в который они могут быть вписаны, или вокруг которого они могут быть описаны. То есть единой их мерой является радиус, равный боковой стороне 0-1 = 0-3 = 1 равнобедренного треугольника, вписанного в четверть круга (Рис.5).

Таким образом, в данном параграфе мы описали гармоничные свойства семейства равнобедренных треугольников и гармонию их симметричного деления с помощью циркуля и линейки на два прямоугольных и равных треугольника.

«Золотое сечение» равнобедренного треугольника

«Золотое сечение», как отмечалось выше, – это гармоничное асимметричное делание некого целого (отрезка) на две не равные части, одна из которых, количественно является средним пропорциональным между целым и двумя его частями и являет собой число 0,6180339…

ПРОБЛЕМА. Как с помощью циркуля и линейки осуществить «золотое сечение» основания и боковой стороны равнобедренного треугольника? Ставился ли когда-либо столь проблематичный вопрос? Если не ставился, следовательно, и не решался.

Чтобы осуществить «золотое сечение» основания равнобедренного треугольника с помощью циркуля и линейки, например, треугольника 1-2-4 (Рис.4), у которого основание равно высоте, производим следующие операции:

1. Ставим ножку циркуля в точку «0» и раствором циркуля 1-4 (Рис.4) описываем полуокружность до пересечения ее с продолжением в обе стороны основания 1-2 данного равнобедренного треугольника (Рис.6). В итоге мы получили равные отрезки:

   1-2 = 0-3 = 0-6 = 1.

   Поэтому, осуществление «золотого сечения» любого из них, равнозначно «золотому сечению» основания равнобедренного треугольника.
   

2. Ставим ножку циркуля в точку 1 (Рис.4) и раствором циркуля 1-4 откладываем на диаметре 3-6 полуокружности отрезок 1-5 равный отрезку 1-4.
3. Соединяем точки 4 и 5 прямой и, таким образом получаем еще один равнобедренный треугольник, у которого, по построению (Рис.4), стороны 1-4 = 1-5 ≈ 1,1180339…
   

   
   

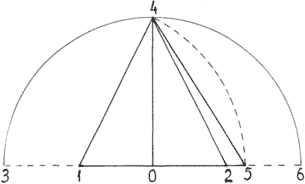
   Рис. 6. «Золотое сечение» радиуса круга равновеликого основанию равнобедренного треугольника

4. Вычисляем отрезки 0-5 и 5-6:
   

   0-5 ≈ 1,1180339 – 0,5 ≈ 0,6180339 – длина стороны

   5-6 = 1 – 0,6180339 ≈ 0,3819661.

5. Вычисляем отрезок 3-5. Длина его равна сумме отрезков 0-3 = 1 и 0-5:
   

   3-5 = 1 + 0,6180339 ≈ 1,6180339.

   Таким образом, на одной прямой (на диаметре круга, радиус которого равен «1») мы геометрически построили оба корня алгебраического уравнения «золотого сечения» .
   

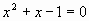6. Вычисляем основание 4-5 равнобедренного треугольника 1-4-5:

   Основание 4-5 является гипотенузой прямоугольного треугольника 0-4-5, один из катетов которого равен мере «золотого сечения» (0,6180339), а другой равен основанию равнобедренного треугольника, т.е равен 1.
   

В согласии с теоремой Пифагора:

.

Построенное число ≈ 1,1755705 – сторона правильного вписанного в окружность пятиугольника. Алгоритм ее построения и вычисления в варианте автора осуществлен по принципу наименьшего действия (круговым переносом). Это очевидно, если сравнить его с известным ранее алгоритмом геометрического построения числа .

Особый интерес для познания представляет отрезок 2-5 (Рис.6): 2-5 ≈ 0,6180339 – 0,5 ≈ 0,1180339. Об этом в другом разделе публикации.

Вывод. Приведенные выше геометрические построения сторон правильных вписанных четырехугольника, пятиугольника и десятиугольника, осуществление «золотого сечения» стороны равнобедренного треугольника и, в том же смысле, радиуса круга, вычисления гармоничных отношений между разными параметрами геометрических фигур, осуществлены значительно проще и образно понятнее, приводимых в существующей математической литературе. Они осуществлены согласно основным принципам гармонии, присущим Природе и могут быть рекомендованы в качестве обязательных знаний при составлении программ образования.

Литература:

1. Платон. Собр. соч. в 4-х т. «Мысль», М., 1994. Т.3. С.457-458.
2. Геометрия. Учебник для 7-9 классов общеобразовательных учреждений. М., «Просвещение». 1995.

Продолжение следует.