«Не думайте, смотрите!»

Л. Витгенштейн, «Философские исследования»

В классической последовательности Фибоначчи каждый последующий член равен сумме двух предшествующих. В этой последовательности элементы связаны двумя типами отношений: структурными, основанными на отношении включения (сумма включает два слагаемых или сумма состоит из двух слагаемых) и линейными: слагаемые предшествуют сумме в развертывании последовательности. В итоге образуется рекурсивная (регрессивная) последовательность. Схематически классическую триаду Фибоначчи можно представить в виде линеаризованного дерева составляющих, используемого для представления синтаксических структур естественных языков:

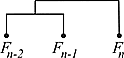
В теории порождающих грамматик такие конструкции именуются левоветвящимися или регрессивными – ступеньки линеаризованного дерева образуют лестницу, ориентированную влево, в отличие от правоветвящихся, прогрессивных структур, для которых характерен «спуск по лестнице» в противоположном направлении (Н. Хомский, В. Ингве). Рассмотренная рекурсия является простейшей. Ее усложнение может осуществляться благодаря увеличению числа суммируемых членов и нарастанию дистантности между элементами суммативного правила. Рассмотрим более сложные варианты.

Начнем с последовательности М. Газале, задаваемой уравнением:

.

При n=3 данное уравнение становится уравнением Падована, корень которого равен 1,325. Этому уравнению соответствует рекурсия вида:

В этом дереве появляется разрыв (вставка, дистантность) между значением суммы и вторым слагаемым. Попытаемся теперь наращивать дистантность d при одновременном увеличении числа рекурсирующих слагаемых n. В качестве затравочных чисел будем использовать числа натурального ряда, начиная с единицы, которые при этом заполнят и дистанционнувю «лакуну» между значением суммы и последним затравочным числом.

А теперь построим таблицу, в которой разместим предельное отношение последующего члена к предыдущему при нарастании n и d.

Таблица 1

Что же мы получили в итоге?

1. В столбце n=2 имеем корни уравнений обобщенного серебряного сечения М.Газале с нарастающей дистантностью рекурсирующих членов.
   

2. Самое интересное содержится в последнем столбце – предельные числа имеют вид корней уравнений обобщенного золотого сечения А.Стахова
   

3. Интересно также и то, что стаховские числа образуют диагональ таблицы
   

4. В столбце n=0 располагаются обобщенные числа Трибоначчи (Файнберга) в расширительном толковании — не только с тремя, но и любым числом рекурсирующих членов
   

Итак, все рекурсии, построенные на базе обобщения Газале, образуют единую систему, в которой центральную роль играет обобщение Стахова. Прибегнув к аналогии с шахматной доской, можно сказать, что последовательность Стахова обладает возможностями ферзя, а последовательности Газале и Трибоначчи совместно — возможностями ладьи.

Но в табл. 1 есть еще одно любопытное свойство, связанное с числом Падована-Газале. Чтобы не заграмождать табл. 1 новой информацией, повторим ее и графически выделим новое свойство – см. табл.1а.

Стаховские диагональные числа тесно соприкасаются с двумя последовательностями, содержащими пары повторяющихся чисел 1,325-1,325, 1,296-1,296, 1,269-1,269, 1,244-1,244 и т. д. Природу и математическое содержание этой последовательности мы пока не раскусили. Пока можно лишь отметить, что она открывается тройным повторением газалевского числа 1,325, при этом ее члены обладают мультипликативным свойством ряда Фибоначчи: центральный член (например, в триаде) равен среднему геометрическому крайних членов. Кроме того, бросается в глаза то, что при переходе от одного числа пары к другому необходимо сделать шаг вправо и спуститься вниз. Это напоминает ход шахматного коня. Такая Г-образность расширяет шахматную интерпретацию таблиц 1 и 1а.

Таблица 1а

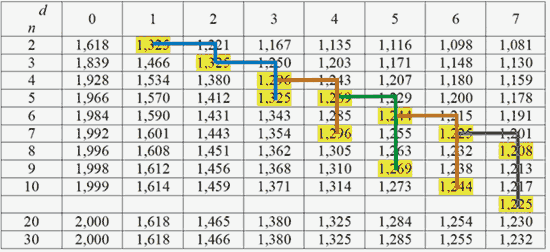
Мы сознаем, что наши наблюдения на данный момент могут рассматриваться лишь как некоторые интригующие констатации. В следующей работе попытаемся им дать рациональное толкование.