Институт Золотого Сечения -Дискуссии

Мартыненко Г.Я.

1. Введение

Mатематические проблемы, связанные с золотым сечением А. П. Стахов (Стахов, 2003; Стахов, 2006) объединил в единую теорию. Представляется, что к этой теории весьма тесно примыкают и ряд элементов понятийного и методического аппарата статистики. Начнем с того, что некоторые ученые включают золотое сечение в число мер центральной тенденции (Венецкий, Венецкая, 1979), а для того, чтобы график отвечал требованиям гармонии, предлагается вписывать его в прямоугольник, в котором высота относится к ширине как 5: 8, что приблизительно равно золотому числу (Митропольский, 1971). Но это лишь внешние признаки родственных отношений между стаховской теорией и статистикой.

В данной статье мы остановимся на более глубинных основаниях, позволяющих осмыслить некоторые приемы статистического анализа с позиций математической теории гармонии

2. Замечательные свойства золотого варианта 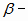функции

При изучении ранговых распределений элементов больших социокультурных систем автор (Мартыненко, 1988) использовал функцию вида

, (1)

где r — ранг элемента совокупности, k — значение соответствующей переменной, N — численность совокупности, q — средняя геометрическая переменной и ее медиана одновременно, а — коэффициент, характеризующий скорость падения ранговой кривой. Этот коэффициент определяется по формуле

где — ранговое среднее, вычисляемое как сумма произведений рангов на соответствующие значения переменной, поделенная на сумму значений последней (Мартыненко, Фомин, 1989). Функция (1) является упрошенным вариантом функции. В теории экстраполяционного прогнозирования она называется замедленной логистической функцией (Haustein, 1960).

Максимальное значение переменной будет равно (при ), а минимальное (при ). Что касается срединного (медианного) значения переменной, то оно, как мы уже говорили выше, будет равно .

Медианное значение переменной s является, с одной стороны, средним геометрическим из значений переменной у «лидера» и «аутсайдера», а с другой, средним геометрическим всего распределения в целом. Легко видеть, что такое соотношение удовлетворяет мультипликативному правилу золотого сечения: в его классической формулировке:

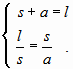
Очевидно также, что аддитивное правило для нашей модели в целом не выполняется.

Предположим, однако, что это правило при определенных условиях выполняется.

Полагая , получаем квадратное уравнение , одним из корней которого будет

Итак, второе правило выполняется только тогда, когда равно золотому числу j.

Из этого следует, что , т. е.

Если пользоваться логарифмами по основанию , то эта формула приобретает вид

Итак, коэффициент при условии выполнения в нашем распределении аддитивного правила золотого сечения целиком определяется численностью совокупности – точнее обратной величиной золотого логарифма этой численности. Во всех остальных случаях аддитивное правило не выполняется и тогда можно говорить о «позолоченном» сечении.

Обратим внимание на то, что при вычислении коэффициентa используется модуль перехода от десятичных логарифмов к золотым, равный 4,78.

Ради справедливости надо сказать, что формулировка золотого сечения в реальной жизни часто используется в редуцированном виде. Так, в классической формулировке используется только мультипликативное правило, а аддитивное выступает или как нечто само собой разумеющееся, или как некоторый фон. В трактовке Фибоначчи в голове угла выступает аддитивное правило, а мультипликативное правило возникает как следствие аддитивного. Более того, иногда аддитивное правило не имеет «физического смысла». Например, в экспериментальной эстетике в духе Фехнера (Fechner,1976; Gilbert, 1939) и его многочисленных последователей весьма популярны измерения соотношения высоты и ширины объектов, но ведь в данном случае сумма высоты и ширины не имеет реального смысла – ни житейского, ни математического.

Заметим также, что поскольку при выполнении аддитивного правила , то , а , т.е. максимальное, медианное и минимальное значения переменной в рамках данной модели образуют убывающую последовательность , если идти от лидера к аутсайдеру или возрастающую, если идти от аутсайдера к лидеру. На логарифмической оси по основанию возрастающая последовательность будет выглядеть так , т. е. члены ряда в золотой логарифмической шкале образуют арифметическую прогрессию с коэффициентом 1.

Обнаруженная нами закономерность может также рассматриваться в контексте теории последовательностей типа Фибоначчи и Люка.

Такие последовательности могут рассматриваться как экспоненциальная зависимость вида , где — a некоторый начальный уровень («затравка»), а

В логарифмическом варианте данная зависимость имеет вид: .

Если , то , а .

Легко видеть, что при t, стремящемся к бесконечности, данная зависимость довольно быстро сходится к последовательности чисел Люка (Воробьев, 1974) (см. табл. 1).

Таблица 1

Числа Люка и Фибоначчи как значения золотой показательной функции

Для перехода от ряда Люка к классическому ряду Фибоначчи необходимо все числа первого разделить на . Обратим внимание также и на то, что t может принимать не только целочисленные, но и непрерывные значения.

Любопытно также и то, что для построения произвольного ряда типа Фибоначчи необходимо знать лишь одно «затравочное» число.

Пусть, например, этим числом будет 0,618, т. е. золотое число. В этом случае мы получим «двойную золотую» последовательность (см. табл.) со сдвигом относительно чисел Люка на одну позицию. Аналогичным образом могут быть использованы и другие замечаельные числа, например, и . Это означает, что в семействе рядов типа Фибоначчи ряд Люка является эталонным, а все остальные ряды являются его вариантами.

А теперь вернемся к функции (1) и приведем два контрастных примера ее использования на практике.

3. Золотые логарифмы футбола

Предположим, что в игровых видах спорта распределение команд по этажам турнирной таблицы в чемпионатах, организованных по круговой системе, регулируется правилом золотого сечения.

Рассмотрим итоги чемпионата Испании по футболу 2004/05 г. Сокращенный вариант итоговой турнирной таблицы может быть представлен в виде рангового распределения, в котором в качестве независимой переменной выступают ранги, а в качестве зависимой — очки, соответствующие этим рангам (см. табл. 2).

Применительно к таблице 2 значения постоянных коэффициентов q и функции (1) будут следующими: а . Как мы говорили выше, коэффициент при соблюдении требования аддитивности может быть определен по формуле . Подставив в эту формулу , получаем , т. е. тот же результат. Это означает, что закон золотого сечения в данном случае действует в полной мере.

Была выдвинута нулевая гипотеза об отсутствии существенных различий между эмпирическими и теоретическими данными. Проверка осуществлялась с помощью критерия согласия вида при числе степеней свободы , где f — число параметров теоретического распределения. Проверка показала, что вероятность критерия весьма велика (0,999), что свидетельствует о высокой степени близости между теоретическим и эмпирическим распределениями.

Таблица 2

Итоги чемпионата Испании по футболу (сезон 2004/2005 гг.)

Ранг	Реальные очки	Теорет. очки		Золотые логарифмы
1	77	82,23	0,355	9,15
2	72	72,95	0,012	8,90
3	71	67,75	0,156	8,75
4	70	64,09	0,545	8,64
5	56	61,22	0,445	8,54
6	55	58,84	0,251	8,46
7	55	56,76	0,055	8,38
8	54	54,90	0,015	8,32
9	52	53,17	0,026	8,25
10	51	51,56	0,006	8,18
11	51	50,00	0,020	8,12
12	48	48,47	0,005	8,06
13	48	46,95	0,023	7,99
14	47	45,41	0,056	7,92
15	46	43,81	0,019	7,85
16	43	42,10	0,019	7,76
17	43	40,22	0,192	7,67
18	41	38,05	0,229	7,55
19	39	35,33	0,339	7,40
20	26	31,34	0,910	7,15
	1045	1045,1	5,658

В заключение отметим, что в шкале золотых логарифмов очки аутсайдера, середняка и лидера, если двигаться от первому к последнему, слагаются в арифметическую прогрессию: 7,15; 8,15; 9,15. Если обратиться к табл. 1, то трем золотым логарифмам в классическом ряде Люка соответствуют числа Люка 29, 47 и 76, золотые логарифмы которых равны, соответственно, 7, 8 и 9. Это означает, что золотой логарифм может быть произвольным числом, не обязательно целочисленным.

Весьма интересным свойством функции (1) является то, что при условии соблюдения правила золотого сечения золотые логарифмы относятся только к трем наиболее характерным точкам турнирной таблицы — очковому багажу лидера, середняка и аутсайдера. В золотой логарифмической шкале только три эти точки ложатся на прямую линию. Остальные точки располагаются вдоль ниспадающей волнообразной вогнуто-выпуклой кривой, пересекающей прямую только в трех упомянутых точках: см. рисунок, приведенный ниже:

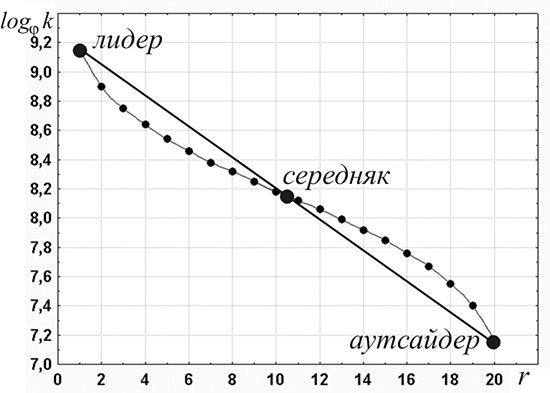
Золотые логарифмы и золотые точки футбольной таблицы

Может сложиться впечатление, что выявленная закономерность относится только к рассматриваемому чемпионату и в массе национальных чемпионатов выполняться не будет.

Рассмотренный нами чемпионат относится к стране с очень высоким уровнем организации футбольного дела. Среди 20 лучших лиг мира Испания занимает высокое
2 место (Мировой футбол, 2005, с. 430–431). Можно ожидать, что в других ведущих лигах мира статистическая картина будет аналогичной.

Ознакомимся с реальной ситуацией в национальных чемпионатах европейских стран в начале XXI века. Начнем с национальных чемпионатов ведущих футбольных стран Европы.

Прежде чем приступить к обсуждению результатов наблюдений, заметим, что численность национальных лиг довольно сильно варьирует. При этом, чем выше численность лиги, тем чаще всего выше рейтинг чемпионата. В рассмотренном чемпионате Испании численность лиги равна 20 командам. Рассмотрим другие равновеликие национальные чемпионаты европейских стран того же сезона. Это чемпионаты Италии (рейтинг 1), Франции (рейтинг 4), Англии (рейтинг 3).

Таблица 3

Золотые логарифмы национальных чемпионатов ведущих футбольных держав Европы
(сезон 2004/05)

		Италия	Испания	Англия	Франция	Среднее
Лидер	Очки	86	84	95	79	86
	Золотой логарифм	9,25	9,20	9,45	9,07	9,25
Середняк	Очки	44	50,5	46,5	49	47,5
	Золотой логарифм	7,86	8,14	7,97	8,08	8,25
	Золотые очки	53,1	51,9	58,7	48,8	53,2
Аутсайдер	Очки	35	28	32	32	31,8
	Золотой логарифм	7,38	6,92	7,19	7,19	7,25
	Золотые очки	32,8	31,8	28,7	30,3	32,9

Данные табл. 3 не опровергают заключений, сделанных выше относительно структуры чемпионата Испании. Чаще всего отклонения возникают из-за наличия в лиге суперклубов, подобных английскому «Челси», которые нарушают гармонию турнира из-за резкого перебора очков, ведущего к недобору очков у клубов, расположенных в центре или в хвосте таблицы. Однако в среднем показатели выравниваются и соответствуют тем выводам, которые мы сделали на материале французского чемпионата. Так, золотой логарифм для усредненного лидера равен 9,25, для середняка – 8,25, для аутсайдера – 7,25, т. е. значения логарифмов образуют строгую арифметическую прогрессию.

Что касается чемпионатов, которые проводятся в лигах меньшей численности, то здесь ситуация складывается следующим образом.

Для большинства чемпионатов с численностью лиги, равной 18 командам, установленные числовые соотношения выдерживаются за исключением тех стран, футбольные федерации которых страдают лиговой гигантоманией, не соответствующей масштабам страны или уровню развития национального футбола (Азербайджан, Уэльс). По мере сокращения численности лиги наблюдается снижение роли гармонической составляющей чемпионата, но эта закономерность имеет чисто статистический характер, поскольку есть довольно много гармонических, но малочисленных чемпионатов.

Попытаемся выявить общую гармоническую картину национальных чемпионатов всех европейских стран. Сделаем мы это следующим образом.

Для каждой страны вычислим золотой логарифм отношения очковых масс, принадлежащих лидерам и аутсайдерам. Если чемпионат удовлетворяет правилу золотого сечения, то это отношение будет равно двум. Отклонения в ту или иную сторону свидетельствует о нарушении гармонии турнирной борьбы.

Этот показатель был вычислен нами для всех стран футбольной Европы, являющихся членами УЕФА для 5 последних сезонов. Результаты вычислений представлены в табл. 4.

Таблица 4

Мера отличия национальных чемпионатов европейских стран в сезонах 2001– 2005 от гармонического эталона H (усредненные данные)

Основные выводы:

1. Очковые накопления лидера, середняка и аутсайдера подчиняются закону золотого сечения, образуя геометрическую прогрессию, а логарифмы их накоплений арифметическую прогрессию для гармонически организованных, сбалансированных футбольных чемпионатов

2. С точки зрения отклонения от гармонического эталона множество национальных чемпионатов европейских стран качественно неоднородно. Если в качестве центра равновесия принять золотое сечение, то верхнее подмножество будет включать преимущественно «традиционные», «старые» европейские страны с налаженной, устоявшейся организацией футбольного дела (таких стран ), а второе — страны, представленные «молодыми» футбольными «державами», возникшими после геополитических преобразований в начале 90-х гг. XX века, главным образом, после распада СССР и Югославии. Во второе подмножество входят также карликовые и малые страны, в которых гармоническая организация спортивных состязаний невозможна в силу ограниченности демографических, территориальных и экономических ресурсов.

3. Верхнее подмножество футбольных стран, в свою очередь, распадается на две группы: страны с отрицательными отклонениями (таких стран только три) и страны с положительными отклонениями от гармонического эталона. Первая группа стран тяготеет к малому перепаду между очковыми массами лидера и аутсайдера, т. е. к максимальному выравниванию класса команд лиги, а во второй группе наряду с малыми отклонениями в положительную сторону, присутствуют и достаточно большие и даже «патологические» отклонения, чуждые чемпионатам традиционных стран.

Ведущие футбольные страны Европы в целом имеют малые отклонения от гармонического эталона. Так, среднее отклонение чемпионатов Италии, Испании, Франции, Англии и Германии составляет лишь 0,16, а 13 рейтинговых стран (в дополнение к перечисленным: Россия, Чехия, Португалия, Греция, Турция, Бельгия, Шотландия, Голландия) — 0,49.

4. О золотом сечении синтаксических структур

По наблюдениям ряда исследователей (например, Адмони, 1965) в первой половине XX века в европейской художественной прозе происходил процесс сокращения среднего размера предложения. Этот процесс В. Г. Адмони назвал движением от громоздкости к портативности. Но портативность и громоздкость могут соотноситься не только с размером предложения, но и с другими экстенсивными (объемными) характеристикам: размером текста, абзаца, словосочетания (например, именного или глагольного), словоупотребления, стихотворной строки и др.

Остановимся на размере предложения. Исследование этой переменной имеет давнюю историю и огромную литературу не только в филологии, но и в теоретической статистике, где эта переменная выступает в качестве образцового распределения, демонстрирующего широту исследовательских приложений статистики (Юл, Кенделл, 1969).

В табл. 5 приведены выборочные данные о среднем размере предложения в русском рассказе указанного периода, а также теоретические значения, вычисленные для функции (1) (Мартыненко, 2007).

Таблица 5

Распределение средних размеров предложения в русском рассказе начала начала XX века (1901 – 1917)

Ранг	Прозаики	Эмпирический	Теоретический	Теоретический золотой
1	М.Кузмин	22,30	23,37	22,32
2	Л.Андреев	21,78	21,42	20,64
3	В.Брюсов	18,99	20,36	19,71
4	А.Чехов	18,90	19,63	19,06
5	А.Куприн	18,54	19,08	18,57
6	А.Амфитеатров	18,30	18,63	18,17
7	С.Елпатьевский	17,92	18,26	18,06
8	А.Хирьяков	17,52	17,93	17,54
9	Г.Гребенщиков	17,36	17,65	17,29
10	Н.Телешов	17,14	17,4	17,06
11	В.Немирович-Данченко	17,02	17,16	16,85
12	М.Горький	16,81	16,96	16,66
13	В.Лидин	16,70	16,76	16,49
14	Е.Чириков	16,44	16,58	16,33
15	И.Бунин	16,40	16,41	16,17
16	В.Ирецкий	16,34	16,25	16,03
17	А.Федоров	16,23	16,10	15,89
18	И.Гарин-Михайловский	16,14	15,96	15,76
19	И.Шмелев	15,92	15,82	15,64
20	И.Василевский	15,90	15,69	15,52
21	Ю.Слезкин	15,86	15,57	15,41
22	Б.Лазаревский	15,64	15,45	15,30
23	Е..Милицина	15,52	15,33	15,19
24	С.Юшкевич	15,50	15,22	15,09
25	Д.Айзман	15,32	15,11	14,99
26	Н.Тимковский	15,20	15,00	14,90
27	А.Толстой	15,06	14,90	14,80
28	С.Сергеев-Ценский	14,92	14,80	14,71
29	Б.Зайцев	14,78	14,70	14,62
30	Н.Крашенинников	14,74	14,60	14,53
31	И.Наживин	14,61	14,51	14,45
32	И.Новиков	14,58	14,41	14,36
33	М.Криницкий	14,52	14,32	14,28
34	Г.Чулков	14,22	14,23	14,19
35	В.Гиляровский	14,18	14,14	14,11
36	М.Пришвин	14,10	14,05	14,03
37	С.Подъячев	14,02	13,97	13,95
38	САуслендер	13,95	13,88	13,87
39	А.Бельский	13,94	13,80	13,80
40	А.Грин	13,80	13,71	13,72
41	С.Скиталец	13,75	13,62	13,64
42	О.Дымов	13,60	13,54	13,56
43	А.Аверченко	13,57	13,46	13,48
44	С.Елеонский	13,56	13,37	13,41
45	К.Тренев	13,40	13,29	13,33
46	А.Соболь	13,39	13,2	13,25
47	А.Ремизов	13,26	13,12	13,17
48	И.Сургучев	13,24	13,03	13,09
49	А.Чапыгин	13,16	12,95	13,02
50	Н.Олигер	13,12	12,86	12,94
51	К.Баранцевич	13,00	12,77	12,86
52	Б.Садовской	12,90	12,69	12,78
53	М.Леонов	12,84	12,60	12,69
54	З.Гиппиус	12,44	12,51	12,61
55	А.Серафимович	11,98	12,41	12,52
56	П.Сурожский	11,96	12,32	12,44
57	В.Вересаев	11,86	12,22	12,35
58	В.Шишков	11,78	12,12	12,26
59	А.Свирский	11,74	12,03	12,17
60	А.Будищев	11,68	11,92	11,07
61	А.Бибик	11,60	11,82	11,97
62	И.Кипен	11,59	11,71	11,87
63	Л.Кармен	11,58	11,60	11,77
64	А.Рославлев	11,50	11,48	11,66
65	С.Кондурушкин	11,26	11,35	11,54
66	Д.Цензор	11,23	11,22	11,42
67	О.Ольнем,	11,18	11,09	11,29
68	А.Каменский	11,12	10,94	11,15
69	А.Измайлов	10,68	10,78	11,01
70	С.Гусев-Оренбургский	10,64	10,61	10,85
71	А.Неверов	10,51	10,42	10,67
72	А.Вербицкая	10,32	10,21	10,47
73	Е.Нагродская	10,28	9,97	10,25
74	Н.Тэффи	10,13	9,69	9,98
75	В.Дорошевич	9,36	9,34	9,66
76	Ф.Сологуб	9,12	8,88	9,22
77	В.Гофман	7,80	8,16	8,52

Было выдвинуто предположение, что данное распределение описывается функцией (1).

Теоретические параметры этого распределения имеют следующую величину: , а .

Параметр может быть вычислен также и с условием соблюдения золотого правила аддитивности:

= 0,111.

Этот результат несколько отличается от того, который был получен при аппроксимации. Возникает естественный вопрос, существенны ли эти различия. Этот вопрос можно прояснить, проверив степень близости теоретических кривых, построенных при двух вариантах коэффициента , с помощью варианта критерия , использованного в Примере 1. Оказалось, что и в том, и в другом случае значения вероятности этого критерия также весьма мала. Это означает, что на распределении средних размеров предложения выполняется не только мультипликативное, но и аддитивное правило золотого сечения в его классическом варианте. В данном случае, естественно, выполняются и правила, по которым строится ряд Фибоначчи: каждый последующий член такого ряда равен сумме двух предыдущих, а среднее геометрическое из крайних членов тройки следующих друг за другом чисел равно второму по порядку следования числу.

Итак, неравномерность распределения средних размеров предложения целиком определяется размером совокупности: чем больше N, тем меньше g. Пусть, например, N=1000, что примерно соответствует числу мастеров русского рассказа ХХ века. Если на этом множестве будет выполняться аддитивное правило золотого сечения, то коэффициент будет равен 0,076. Допустим, при этом средний геометрический размер предложения останется тем же, что и в начале века — 13,80. Тогда при заданном значении коэффициента
g = 0,076 максимальное и минимальное значения останутся теми же. Например, для лидера это число будет равно

.

Из этого следует, что при постоянном значении среднего геометрического q и соблюдении правила аддитивности, распределение остается постоянным с тем лишь отличием, что область изменения аргумента заселяется большим числом беллетристов. Крайние значения среднего размера предложения при соблюдении правила аддитивности целиком определяются величиной среднего геометрического q. Пусть оно равно 10. Тогда максимальное значение l будет равно , а минимальное — . Если же q равно 20, то максимальное значение будет равно 32,36, а минимальное — 12,36.

Но все сказанное, повторяем, относится лишь к случаю соблюдения правила аддитивности, которое имеет шанс на это только при условии целостности литературно-художественной системы, что, по-видимому, свойственно рассмотренной нами. Возможно, это будет соблюдаться и для других систем, отвечающих этому жесткому требованию. Известно, например, что в 20-е гг. XX века наметилась резкая тенденция к сокращению размера предложения. Так, в прозе Лидии Сейфуллиной он едва дотягивал до 5 слов. Если этот размер считать для данной эпохи минимальным, то при описанных выше ограничениях средний геометрический размер предложения для эпохи в целом составит , а для максимального среднего размера — единиц. Так ли это будет на самом деле, узнает лишь тот, кто проведет первым исследование на материале данной эпохи. Скорее всего, в данную эпоху эти пропорции соблюдены не будут, так как некоторые писатели, пришедшие из предреволюционной эпохи, останутся верными прежней манере писать длинными предложениями. Однако в любом случае, предложенная модель может рассматриваться как некоторый эталон, при наложении которого на конкретный материал ёболее четко просматриваются структурные границы литературно-художественных систем в синхронии и дихронии.

Что касается других экстенсивных переменных, то по нашим расчетам что с повышением языкового уровня величина коэффициента возрастает. Это означает, что свобода индивидуального выбора весьма мала на лексико-морфологическом уровне (размер словоупотребления) и весьма велика на межфразовом уровне (размер абзаца). На собственно синтаксическом уровне свобода выбора и ограничения на эту свободу находятся в равновесном состоянии (размер предложения). Именно поэтому теоретическая модель здесь работает в «золотом» режиме. Что касается других экстенсивных параметров (размер слова и размер абзаца) (Мартыненко, 2007), то для них выполняется только мультипликативное свойство золотой пропорции и поэтому здесь можно говорить лишь о «позолоченном» сечении.

5. Заключение

1. Золотой вариант функции обладает мультипликативным свойством золотой пропорции, а при условии близости коэффициента к золотому логарифму численности совокупности также и аддитивным свойством.

2. Средняя геометрическая распределения является одновременно его медианой, т. е. эта «гибридная» характеристика обладает по оси рангов свойством зеркальной симметрии, а по оси зависимой переменной — свойством золотой симметрии.

3. При выполнении на совокупности закона золотого сечения максимальное и минимальное значения переменной целиком определяются величиной среднего геометрического всего ряда.

4. Минимальное, медианное и максимальное значения переменной золотого варианта функции образуют золотую последовательность, описываемую показательной функцией, быстро сходящейся к последовательности Люка. При этом ряд Люка является эталонным, а все ряды типа Фибоначчи являются его вариантами.

5. Предложенная модель обладает значительным прикладным и междисциплинарным потенциалом (от филологии до спорта).

Литература

Адмони В.Г. Основы теории грамматики. Л., Наука, 1955.

Венецкий И.Г., Венецкая В.И. Основные математико-статистические понятия и формулы в экономическом анализе. М.: Статистика, 1979.

Воробьев Н.Н. Числа Фибоначчи. М: Наука, 1978.

Кенделл Дж. М., Стьюарт А. Теория распределений. М.: Наука, 1966.

Мартыненко Г.Я. Основы стилеметрии. Л.: Изд-во ЛГУ, 1988.

Мартыненко Г.Я., Фомин С.В. Ранговые моменты // Научно-техническая информация. Серия 2, 1989 №2. С. 9–14.ё

Мартыненко Г.Я. Числовая гармония текста: Введение в лингвистическую нумерологию. М., 2007 (в печати).

Мировой футбол 2005. Справочник / Составитель И. В. Гольдес. // М, Олимпия Пресс, 2005.

Митропольский А.К. Техника статистических вычислений. М.: Наука,1971.

Стахов А.П. Сакральная геометрия и математика гармонии // Проблеми гармонiї, симетрiї i золотого перетину в природi, науцi та мiстецтвi. Вiнниця: Вiнницький державний аграрний унi верситет, 2003. С. 8–26.

Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. СПб.: Питер, 2006.

Fechner G.T. Vorschule der Дesthetik. Leipzig: Breitkopf & H дrtel, 1876.

Gilbert K. & Kuhn H. A History of Дesthetik. London: Thames and Hudson, 1939.

Наustein H D. Prognosevervahren. Berlin, 1960.

[Обсуждение на форуме «Наука»]