Физическая сущность способа гравилевитации вытекает из причин гравитации масс тел, находящихся в вакууме. Физический смысл слова «вакуум» определяется его свойствами: диэлектрической проницаемостью вакуума e=1(СГС), магнитной проницаемостью m=1(СГС), гравитационной постоянной Ньютона G=6,67Ч10^-8cм³Чг^-1Чсек^-2(СГС), гравитационной проницаемостью вакуума или его жёсткостью К, равной обратной гравитационной постоянной Эйнштейна К=С²/G (C- скорость света), волновым сопротивлением вакуума »370 Ом (СИ), степенью электрон-позитронной поляризации вакуума, зависящей от постоянной тонкой структуры вакуума a=1/137, геометрией (симметрией) Евклида плоского пространства в виде многообразия точек вакуума и искривлением (деформированием) этого пространства, которое описывается неевклидовой геометрией Римана, геометрией Картана, конформной геометрией, проективной геометрией и т.д.

Причина гравитации имеет несколько эквивалентных языков описания, используемых ниже. Так, например, притяжение двух точечных массивных тел объясняется созданием разности давлений квадрупольных деформаций вакуума, где вакуум рассматривается как упругая среда с упомянутой выше жёсткостью, выраженной через линейную плотность массы-энергии К~10²⁸г/cм.

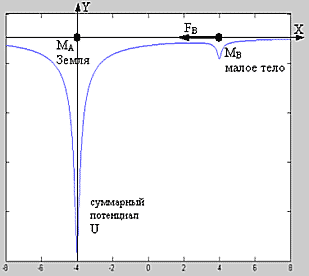
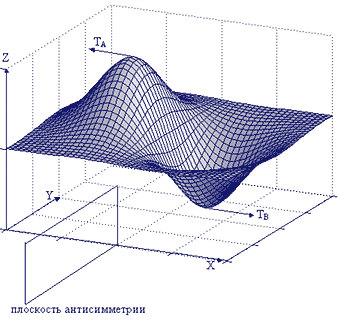
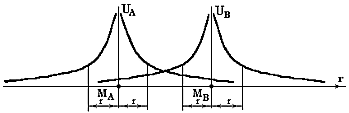
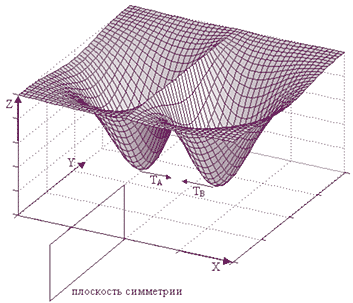
Фиг. 1 - график ньютонова гравитационного потенциала двух точечных масс Увеличить >>>

Ньютоновы потенциалы этого гравитационного поля или поля деформаций
U_A=GЧM_A/r_A, U_B=GЧM_B/r_B для точечных масс М_А=М_В=М показаны на фиг.1.

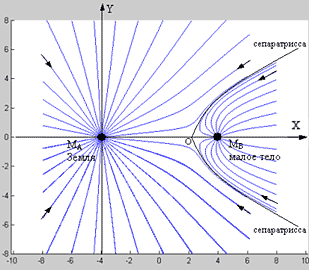
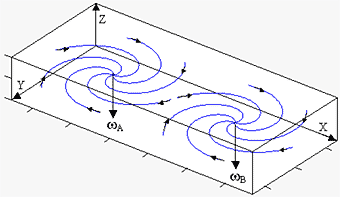
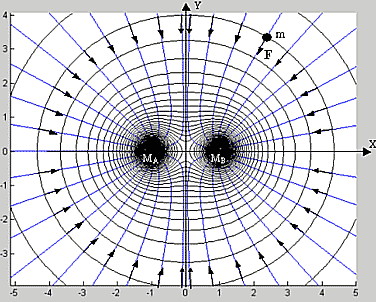
График силовых линий суммарной напряжённости деформации или гравитационного поля, или сил веса F приведён на фиг.2, где пробное тело — индикатор поля имеет бесконечно малую массу m, не возмущающую суммарное поле.

Фиг. 2 - график силовых линий ньютонова гравитационного поля двух точечных масс. Увеличить >>>

В соответствии с законом Ньютона для двух точечных гравити­рую­щих тел (см. фиг.2) гра­ви­тацион­ное поле имеет квад­руполь­ную сим­метрию (геомет­рию), где сущест­вует точ­ка О рав­нове­сия сил поля (точка Лагра­нжа или точка либ­рации). В облас­ти либ­рации (грави­леви­та­ции) грави­тацион­ное поле ском­пен­сиро­вано и реализуется состояние относительного равновесия для пробной массы m: в отсутствии начального отклонения тело m двигается равномерно с постоянной скоростью. При отсутствии начальной скорости и начального отклонения тело m остаётся в точке О бесконечно долго. В других случаях оно совершает малые гармонические колебания: для малого продольного движения по оси Х имеем схему на фиг.3.

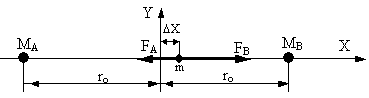Фиг. 3 - схема продольных движений двух гравитирующих точечных масс.

Согласно закону Ньютона для М_А=М_В=М имеем:

F=mЧg=mЧDC^"=GЧM_AЧm/(—r₀+DC)²+GЧM_BЧm/(r—D C)² »
»GЧMЧmЧ[—(1/r_o²—2D C/—r_o³)+1/r_o²— 2DC/r_o³]= —4ЧGЧMЧ mЧDC/r_o³.

или с точностью до D C ~ 0 получим (после сокращения на m)

D C " + 4GЧ m /ro3 Ч D C »0, (~D C<<ro),

(1)

где 4GЧ m / r_o³ — механическая линейная жёсткость силовой линии гравитационного поля (но не вакуума).

Фиг. 4 - схема поперечных движений двух гравитирующих точечных масс.

Аналогично для поперечного малого движения пробного тела m по схеме, указанной на фиг. 4, имеем следующее уравнение Ньютона.

F=mЧ g=mЧ D Y^"= GЧ MЧ [- m / ((- r₀)²+D Y²) - m / (r₀² - D Y²)] Ч cos(j),

cos(j)=D Y/r₀=D Y/((- r₀)²+D Y²)^1/2, тогда

D Y^"= - GЧ MЧ [1 / r₀² - 2Ч D Y /r₀³ + 1 / r₀² - 2Ч D Y /r₀³ ] Ч D Y/r_{0 »}

» - GЧ MЧ [2Ч D Y / r₀³ - 4Ч D Y² /r₀⁴]

или с точностью до D Y² ~ 0 имеем

D Y" + 2Ч GЧ m /ro3 Ч D Y » 0.

(2)

Из сравнения уравнений (1) и (2) видно, что даже в классическом случае ньютоновой механики жёсткость вакуума по грав. полю на продольной оси OX и в поперечной плоскости YOZ различна: 4Ч GЧ m /r_o³ и 2Ч GЧ m /r_o³ соответственно, что очевидно, так как для продольного движения пробной массы m силовые линии грав. поля сгущаются вокруг продольной оси, а для движения по поперечной оси эти линии сгущаются к поперечной плоскости, поэтому жёсткость поля в первом случае больше, чем во втором.

Увеличить >>>

Фиг. 5 - график силовых линий ньютонова гравитационного поля двух точечных масс различной массы. Увеличить >>>

Упомянутое состояние относительного равновесия вблизи точки либрации (гравилевитации) следует из (1) и (2): при D C =D Y=0 ускорения D C ^"=D Y^" =0, т.е. пробная масса m находится в состоянии покоя. Если массы двух гравитирующих тел сильно отличаются, например Земли M_A и другой малой массы M_B, то область либрации (компенсации) или гравилевитации находится вблизи центра масс малого тела M_B, именно данный факт используется в способе гравилевитации, описанном в заявке на изобретение. Сепаратриссы суммарного поля прижимаются к оси OX как показано на фиг. 5.

В рамках общей теории относительности гравитация произвольных масс-энергий описывается уравнением Эйнштейна

K_ik=(8ЧpЧG/c²)ЧT_ik или

(c²/(8Чp ЧG))Ч K_ik=T_ik в такой форме оно соответствует уравнению упругости Гука в дифференциальной форме для тензора энергии-импульса или напряжения (давления) среды T_ik и тензора кривизны пространства (многообразия точек) K_ik этой деформированной среды (вакуума).

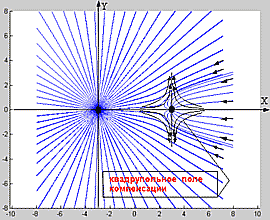
На фиг. 5 видно быстрое нарастание напряжения (давления) силовых линий поля за малым телом M_B (вне интервала АВ),

Увеличить >>>

Фиг. 6 - график силовых линий ньютонова гравитационного поля двух точечных различной масс и компенсирующего поля. Увеличить >>>

где неоднородность поля (grad(U)=g) возрастает в объёме пространства вблизи массы M_B. Поэтому задача компенсации грав. поля в этом объёме состоит в создании квазиоднородности суммарного поля, состоящего из грав. поля Земли, грав. поля малого поля и компенсирующего поля с квадрупольной симметрией показанной на фиг. 6.

Именно в таком случае можно реализовать локальную квазиоднородность в объёме пространства вблизи малого точечного тела или в объёме малого протяжённого тела M_B, эта ситуация создавалась в эксперименте путём генерации в указанном объёме ЭМ-солитонов вакуума.

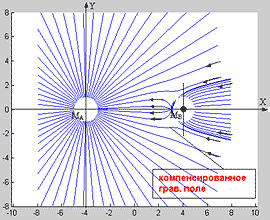
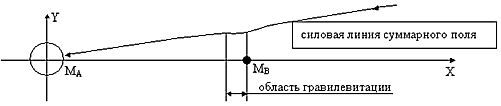
На фиг. 6 видно как при суммировании грав. поля Земли и квадрупольного поля компенсации в области малой массы M_B происходит искривление радиальных силовых линий поля Земли, так что они становятся параллельными оси OX, поэтому (см. нижний график фиг. 6) сила гравитации F = grad(U) » 0, так как изменение грав. поля вдоль радиуса обусловлено расхождением силовых линий F ~ 1/r² и когда локально расходимости нет, то grad(U) » 0 в этой области. Более детально механизм деформации одной силовой линии суммарного поля в плоскости XAY показан на фиг. 7, где показана область отсутствия расходимости (область гравилевитации). Из сравнения фиг. 5ё 7 видно, что в результате компенсации жёсткость вакуума возрастает, то есть локально не деформируется, тогда напряжённость поля становится равной нулю.

Фиг. 7 - график деформации одной силовой линии грав. поля в процессе компенсации этого поля. Увеличить >>>

Важно отметить, что с геометрической точки зрения общей теории относительности Эйнштейна локальное отсутствие гравитационного поля означает локальную реализацию в этой области плоского (псевдоевклидова) 4-х мерного пространства-времени Минковского, тензор кривизны Эйнштейна которого К_ik=0 [7]. То есть квадрупольная деформация упругого вакуума отсутствует. В самом общем случае для деформаций и напряжений любой природы в соответствии с законом Гука в пространствах любой размерности можно сказать следующее: деформации (напряжения) от двух источников (двух тел), описываемые истинными тензорами (векторами), симметричные относительно зеркального отражения в плоскости симметрии двух тел (как например полярные векторы), создают эффект притяжения (сближения этих тел).

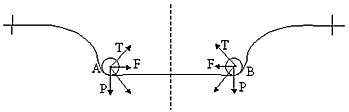
Фиг. 8 - схема процесса притяжения двух одномерных солитонов изгибных деформаций упругой струны. Увеличить >>>

Такой же эффект притя­жения соз­дают дефор­мации, описы­ваемые псевдо­тен­зо­рами, например, аксиаль­ными векто­рами (враще­ния, винтовых сдвигов, крутиль­ных сдвигов). Но эти псевдо­тензоры анти­сим­мет­рич­ны от­носи­тельно указанной зеркальной симметрии источников этих деформаций (двух тел). Данный факт следует из самых общих симметричных свойств фрактальных многообразий, созданных множеством состояний указанных деформаций с притягивающим аттрактором [1] в центре симметрии двух источников деформаций. Иллюстрация эффекта гравитации в различных размерностях среды показана на фиг.8ё 13.

Фиг. 9 - схема процесса притяжения двух взаимодействующих двумерных солитонов изгибных деформаций поверхности. Увеличить >>>

Например, нелинейная струна и два её солитона А, В изгибных деформаций, описываемых уравнением Клейна-Гордона с кубической нелинейностью [2], создают деформацию изгиба с напряжением струны в виде вектора Т.

Между А и В кривизна струны равна 0 и напряжение равно 0 согласно закону Гука. Снаружи кривизна и напряжение не нулевые, что создаёт эффект притяжения.

Двумерный аналог одномерной струны для двух солитонов прогиба упругой поверхности показан на фиг.9, где источники прогибов с тензорами деформаций Т_А = Т_В находятся в лунках А и В.

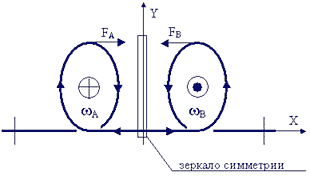
Фиг. 10 - схема процесса притяжения двух солитонов спиральной деформации упругой струны. Увеличить >>>

Иллюстрация притяжения крутильных деформаций, которые описываются псевдотензорами (псевдовекторами), для плоских витков спирали показана на фиг.10. Где изображены два упругих витка спирали А и В в плоскости чертежа XOY, ориентация витков различна относительно этой плоскости и помечена стрелками Е и Q ортогональными плоскости XOY, направленными в разные стороны вдоль оси Z. Однако, относительно зеркала в плоскости YOZ эти правые и левые крутильные продольные деформации, определяемые псевдовекторами w_А и w _В, симметричны (вихри согласованы).

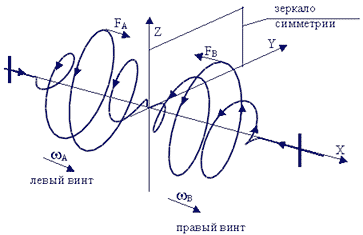
Фиг. 11 - схема процесса притяжения в 3-х мерном пространстве двух одномерных солитонов винтовой деформации среды. Увеличить >>>

Объёмные продольно-поперечные крутильные (спиральные) деформации винтового сдвига в виде двух упругих пружин А и В правой и левой спи­раль­ности пока­заны на фиг.11. Эти два солитона согла­сован­ного крутильно-винтового сдвига, опи­сы­вае­мые нелинейным солитон­ным уравнением sin-Гордон с тригономет­рической нелинейностью, притягиваются друг к другу [2] и являются одно­мер­ным аналогом элек­тричес­кого притяже­ния двух противо­положно заряженных тел. При совмещении деформаций А и В они исчезают (аннигилируют аналогично электрону-позитрону).

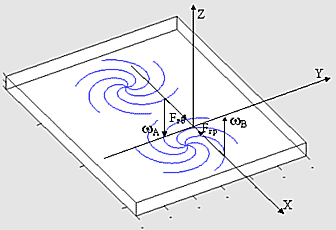
Фиг. 12 - схема процесса притяжения двух двумерных солитонов крутильного сдвига поверхности. Увеличить >>>

На фиг.12 приводится пример двух согласованных вихрей крутильных (аффинных) деформаций в плоскости P, которые имеют разное направление кручений, задаваемых псевдовекторами w_А и w_В ортогональными плос­кости Р.

Например, комбинация линейных деформаций изгиба и спирального (винтового) сдвига на фиг.8 и фиг.11 описывает притяжение двух источников с разной геометрией.

Комбинация двумерных деформаций прогиба и крутильного сдвига на фиг.9 и фиг.12 описывает гравитацию двумерного потенциального источника и вихреисточника деформаций, которые описываются тензором и псевдотензором деформации. Они имеют разные модули упругости (жёсткости) и разные силы притяжения аналогично электрическим и гравитационным взаимодействиям.

Так, исследование топологической (групповой) симметрии системы уравнений Максвелла-Дирака-Эйнштейна для фермионов (электронов, протонов, нейтрино), выполненное в [3], выявило комбинацию объёмных деформаций вакуума типа квадрупольных деформаций геометрии, описываемой тензором кривизны Эйнштейна К_ik и винтовой деформацией этого вакуума, описываемого псевдотензором кривизны кручения Картана-Риччи W_ik. Винтовые деформации на фиг.13 в виде двойной спирали (конхоиды) образуют стабильное образование в форме сверхустойчивого шарового вихря, где внутренний вихрь согласован с наружным вихрем, и представляют собой соответственно правые и левые спиральные напряжённые пружины, которые расталкиваясь в тоже время компенсируют друг друга, устраняя разрыв шарового вихря, то есть электрона и протона, делая их устойчивыми.

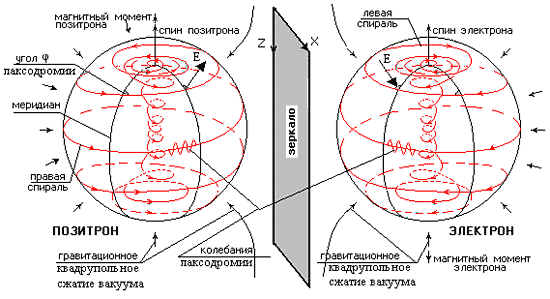Фиг. 13 - схема гравитационного взаимодействия двух трёхмерных солитонов крутильных деформаций и квадрупольных деформаций (чистого сдвига) 3-х мерной среды.

Для понимания сути изобретения важно отметить, что вихревая нить двойной спирали указанного шара образует заузленную петлю многолистника (конкретно~10²²-листника), а непрерывное множество этих нитей на сфере образует поверхность заузленного тора (торического узла), у которого ~ 10²² витков. Непрерывное множество таких торических поверхностей, вложенных друг в друга по направлению к центру шара, образуют вихревое пространство электрона в виде двойного шарового вихря деформации вакуума, который является солитоном решения указанных выше уравнений. Снаружи электрона-солитона вихрь деформации постепенно затухает на бесконечности, метрика пространства становится плоской псевдоевклидовой.

В гравилевитации с помощью фокусировки электромагнитных солитонов используется именно это свойство геометрии двойного вихря: при движении точечного электрона излучается классическая электромагнитная волна Максвелла-Герца, однако при движении электрона-солитона с его сложной внутренней геометрией излучается поле электромагнитных солитонов вакуума, причём излучённое поле повторяет геометрию электрона-солитона, то есть представляется в виде заузленных торов (торических узлов) электрического и магнитного поля, в отличие от классических электромагнитных волн, имеющих геометрию обычных торов. Именно излучение электромагнитных солитонов вакуума (или торических узлов ЭМ-полей) генерируется в устройстве антенн, описанных в данной заявке на способ гравилевитации.

Всестороннее сжатие вакуума (локально квадрупольное), как электрона-солитона, так и электромагнитного солитона, индуцируется сжатием шарового вихря (как пружины при её скручивании), что создаёт электромагнитную массу в виде полной энергии mЧc² этой модельной пружины. Именно квадрупольная деформация всестороннего неоднородного сжатия вакуума определяет гравитационное поле Ньютона вне этого шара в форме гравитационного поля электрона, протона, атома...

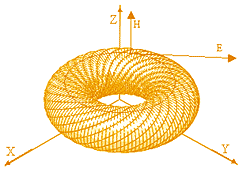
Качественно комбинация этих деформаций изображена на фиг.13, где показана одна двойная вихревая нить на сфере электрического радиуса электрона R_e=e²/m_ec² и распределение вектора ускорения свободного падения (напряжённости g гравитационного поля вблизи электрона и позитрона). Вихревая линия на сфере является логарифмической спиралью (локсодромией), угол j её наклона по отношению к меридиану постоянен для сферы фиксированного радиуса. Величина угла j называется скалярным потенциалом электрического поля Кулона на выбранном радиусе. На бесконечности угол j =0 (локсодромия становится направленной по меридиану) и электрическое поле отсутствует, тогда j=1/R=0. Такое скалярное поле j сферически симметрично по свойству локсодромии.

Напряжённость электрического поля, определяемая по действию поля на пробный электрический положительный заряд равна Е=grad(j) (производная берётся вдоль радиуса). На фиг.13 показано, что вектор Е исходит с поверхности сферы положительно заряженного тела (знак определяется направлением вихря или угла j локсодромии), например, позитрона или протона, и входит в поверхность отрицательно заряженного тела, где знак вихря и угла j зеркально противоположен знаку вихря и угла j положительно заряженного тела. Спиральные нити вихря закручены в электроне (позитроне) на N_e~10²⁰ витков в шаре с электрическим радиусом электрона R_e~10^-13 см, тогда на комптоновском радиусе электрона R_h=h/m_ec~10^-11см число этих витков увеличивается в 1/a » 137 раз и становится равным N_h~10²², точные значения этих величин приведены в [4]. Скручивание вакуума на N_e~10²⁰ витков уменьшает его линейную жёсткость c²/G=m₀/R₀~10^-5г/10^-39см=10²⁸г/см по энергии в N_e²=10⁴⁰ раз, где m₀~10^-5г — масса планкеона (кванта массы — энергии вакуума), R₀=10^-33cм длина планкеона (кванта линейного размера вакуума).

Крутильное размягчение сверхжёсткого вакуума в объёме электрического или комптоновского радиуса определяет массу электрона m_e из закона сохранения момента импульса и кинетической энергии вакуума:

m_0Ч cЧ R₀=N_hЧ m_eЧ cЧ R_h/N_h=m_eЧ cЧ R_h или

m_0Ч c^2Ч R₀=N_hЧ m_eЧ c^2Ч R_h/N_h=m_eЧ c^2Ч R_h, m_e=m_0Ч R⁰/R_h^.

Указанное изменение жёсткости вакуума путём генерации в нём ЭМ-солитонов лежит в основе описываемого способа реализации гравилевитации.

Изменение жёсткости вычисляется по формуле:

К=с2/G=m0/R0=NeЧ me/Re/Ne=Ne2Ч Re~1040Ч Re,

(3)

где R_e=m_e/R_e - очень маленькая жёсткость вакуума в объёме электрона, обусловленная многовитковой деформацией (многовитковой пружиной), однако, полная энергия электрона-солитона сохраняется, так как энергия пружины пропорциональна квадрату числа витков N_e². Этот факт выражен в формуле (3). Из этой формулы следует, что энергия гравитационного взаимодействия в 10⁴⁰ раз слабее электрического взаимодействия, поэтому квадрупольные деформации вакуума (то есть гравитация) не так сильно изменяют давление вакуума, как электрические поля (обусловленные крутильными деформациями). Из формулы (3) это следует тривиально:

1=N_e^2Чm_eЧG/c^2ЧR_e.

Умножим левую и правую части на m_e и получим:

me=Ne2Ч GЧ me2/c2Ч Re,

(4)

но m_e определяется электрической энергией электрона как

e²/R_e=m_eЧ c² или m_e=e²/c^2Ч R_e,

что после подстановки в (4) даёт соотношение:

e²/R_e=N_e^2Ч GЧ m_e²/c^2Ч R

или для энергий

e²/R_e=10^40Ч GЧ m_e²/R_e,

где слева стоит выражение собственной электрической (крутильной) энергии электрона, а справа - гравитационной (квадрупольной) энергии на радиусе R_e.

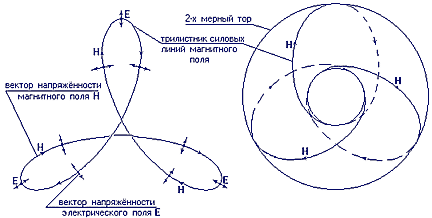
Фиг. 14 - конфигурация поля ЭМ-солитона в форме торического узла. Увеличить >>>

При компенсации электрического поля в электрически нейтральных веществах, остаётся малая гравитационная (инерционная) энергия (m_eЧ v²/2). Кроме того, квадрупольную деформацию вакуума невозможно по симметрии полей компенсировать крутильными деформациями (т.е. электрическим полем) и даже квадрупольными электрическими и магнитными полями, потому что эта квадрупольность (электрическая) есть квадрупольность крутильных сдвигов, которые по симметрии не соответствуют квадрупольным деформациям (чистому сдвигу) гравитационного поля. Поэтому в ЭМ-солитонах вакуума, генерированных в разработанной антенне, реализуется именно квадрупольная деформация чистого сдвига, что необходимо для компенсации гравитации. Конфигурация поля ЭМ-солитона в виде торического узла показана на фиг.14, где квадрупольная деформация поля в центре узла в пересечении силовых линий очень большая и по энергии достаточна для компенсации квадрупольной деформации вакуума в виде гравитационного поля.

Как и в случае притяжения деформаций, так и в случае антигравитации факт отталкивания следует из самых общих симметрийных свойств фрактальных многообразий, созданных деформациями вакуума с отталкивающим аттрактором [5] в центре симметрии антигравитирующих тел. Однако, в противоположность притяжению, для деформаций напряжений, описываемых истинными тензорами (векторами), возникает отталкивание, если они антисимметричны относительно плоскости симметрии двух источников деформации, и, наоборот, для деформаций, описываемых псевдотензорами (псевдовекторами) вращения, крутильных сдвигов, винтовых сдвигов и т. д., так же возникает отталкивание, если они становятся симметричными относительно плоскости симметрии двух источников деформации.

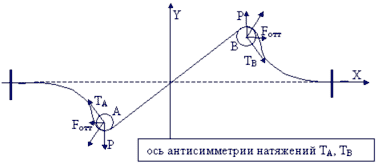
Фиг. 15 - схема процесса отталкивания для двух одномерных солитонов антисимметричных изгибных деформаций. Увеличить >>>

Иллюстрация вы­ше­изложен­ного факта приведена на фиг.15 в форме графика ана­ло­гич­но­го фиг.8 для одномерного изгиба от двух солитонов А и В, но при анти­сим­мет­рич­ной деформации стру­ны. По физической природе векторы сил Р_А и Р_В источников деформаций, а так же векторы напряжений струны Т_А и Т_в — полярные векторы, но созданная ими антисимметрия профиля (деформации изгиба), делает эти векторы антисимметричными относительно нарушенной зеркальной симметрии в плоскости YOZ ^ OZ. Это приводит к появлению сил отталкивания F_от или антигравитации антисимметричных солитонов деформаций А и В в соответствии с солитонным уравнением Клейна-Гордона с кубической нелинейностью.

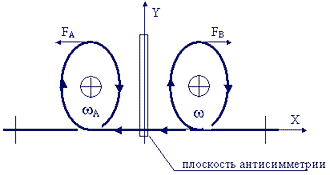
Фиг. 16 - схема процесса отталкивания для двух одномерных солитонов спиральной деформации. Увеличить >>>

Иллюстрация отталкивания крутильных деформаций, описываемых псевдотензорами (псевдовектрами), плоских петель, аналогичных фиг.10, приведена на фиг.16, где вихри не согласованы.

На фиг.16 изображены две правые (левые) крутильные деформации в виде спиралей, описываемые псевдовекторами w _А и w _В, они соответствуют солитонам уравнения sin-Гордона. При начальном максимальном сближении в центре симметрии солитонные петли разбегаются к краям аналогично солитонным прогибам фиг.15.

Фиг. 17 - схема процесса отталкивания в 3-х мерном пространстве двух одномерных солитонов винтовой деформации. Увеличить >>>

Две трёхмерные спирали, анлогичные фиг.11, но одинаковой спиральности, например, правого винта, будут отталкиваться как два одинаковых электрических заряда [2]. Вихри их деформаций не согласованы (см. фиг.17). На фиг.17 по сути изображена одна расщеплённая пружина, витки которой стараются оттолкнуться под действием внутренних крутильных нап­ряже­ний w_А и w_В как и на фиг.16.

Существуют двумерные деформации прогиба и крутильного сдвига поверхности показанные на фиг.18 и фиг.19 в виде солитонов деформаций, которые от­талки­вают­ся, тогда как на фиг.9 и фиг.12 проил­люс­три­рован противо­полож­ный случай притяжения.

Фиг. 18 - схема процесса отталкивания в 2-х мерном пространстве двух двумерных солитонов изгибных деформаций. Увеличить >>>

На фиг.18 показаны два антисимметричных прогиба: один вниз — РА, а другой вверх — РВ относительно оси Z, которые отталкиваются.

Фиг. 19 - схема процесса отталкивания в 2-х мерном пространстве двух солитонов крутильной деформации. Увеличить >>>

Два несогласованных вихря крутильной деформации на фиг.19 отталкиваются, хотя их псевдовекторы деформации w А и w В симметричны относительно плоскости YOZ.

В трёхмерном пространстве (см. фиг.20) для деформаций винтового сдвига в шаровом вихре (аналогично фиг.13) существует напряжение F_от отталкивания, определяющее электрическое отталкивание. Квадрупольная деформация сохраняется, обуславливая гравитацию масс А и В.

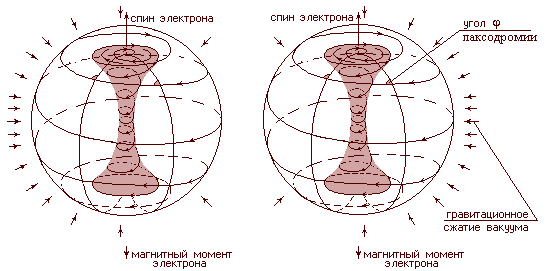Фиг. 20 - схема процесса отталкивания в 3-х мерном пространстве для крутильных деформаций среды и процесса притяжения для квадрупольных деформаций двух 3-х мерных солитонов аналогов элементарных частиц.

Следует отметить, что используемые геометрические термины «сжатие», «крутильный сдвиг», «квадрупольные деформации» взяты из топологических свойств торов, торических узлов, гомологических трёхмерных сфер S³ [6], а динамическое понятие «силы» есть отображение факта движения источника указанных геометрических деформации с ускорением по формуле Ньютона F=mЧ a. Связь геометрических (топологических) свойств пространств и динамических параметров (в виде силовых полей) не тривиальна.

Так, например, топологическая склейка вдоль силовых линий электрического поля шаров на фиг.13 порождает сферическую гиперповерхность S³ (то же самое получается при склейке двух полноторий по меридианам и параллелям внутреннего и внешнего торов). Однако топологическая переклейка этих двух торов по скрученным параллелям превращает эту гиперсферу в топологическое линзовое факторпространство, в частности в проективно евклидово (плоское) 3-х мерное факторпространство RP³. Такой скрученный тор материализуется в конфигурацию силовой электромагнитной волны Максвелла, двигающейся в указанном плоском 3-х мерном факторпространстве, созданном самим электроном. Топологическая перестройка пространства RP³ по трилистнику, то есть переклейка указанных двух торов полнотория сферической гиперповерхности S³ по узлу трилистника снова изоморфна этому S³ [6]. То есть тор (торический узел) опять индуцирует гиперповерхность 3-х мерной сферы с геометрией Римана, что с точки зрения общей теории относительности Эйнштейна эквивалентно появлению силового поля гравитации [7]. Именно такую геометрию торических узлов материализуют ЭМ-солитоны, которые генерируются в разработанной антенне. Существование 3-х мерной гиперповерхности S³, описывающей геометрию вакуума вокруг и внутри электрона и ЭМ-солитона, определяет процесс всестороннего сжатия многообразия точек вакуума вокруг них, а следовательно и локальный квадрупольный сдвиг в каждой точке этого многообразия, что эквивалентно наличию динамического гравитационного поля у этих источников деформаций. Для стационарной деформации пространства масса покоя электрона-солитона постоянна, однако масса покоя ЭМ-солитона, обусловленная топологией пространств с делителем нуля [8], переменна и пульсирует синхронно с пульсацией заузленного электрического и магнитного поля торического узла [9], благодаря чему скорость движения ЭМ-солитона бывает меньше и больше скорости света в вакууме, геометрия которого является сферическим гиперпространством S³.

Во всех описанных выше деформациях среды различной размерности увеличение жёсткости среды (или давления) между телами способствует отталкиванию, размягчение среды (уменьшение жёсткости) или уменьшение давления между ними определяет притяжение (гравитацию). Именно это изменение давления вакуума с помощью ЭМ-солитонов за счёт присущей им квадрупольной деформации чистого сдвига, обусловленного топологией заузленного электромагнитного поля, используется при создании гравилевитации.

Указанная разность давлений в рамках квантовой теории поля в виде напряжённости гравитационного поля обусловлена обменом продольных (или виртуальных) гравитонов (квантов гравитационного поля) с квадрупольной симметрией поля [10], аналогичной фиг.2. Расчёт этой силы тривиален: импульс продольного гравитона с длиной волны l равен p=h/l; излучают его источники деформации (массы М_А и М_В) как «абсолютно чёрное тело» по закону Джинса с плотностью вероятности dl /l, тогда сила давления или гравитации (фиг.21)

,

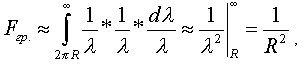—  что даёт закон Ньютона.

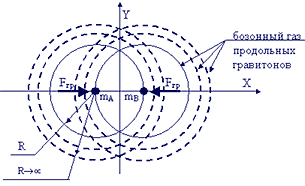
Фиг. 21 - схема процесса гравитации в модели давления гравитонного газа. Увеличить >>>

Орбиты непрерывного распределения этих обменных гравитонов бозонного газа показаны на фиг.21.

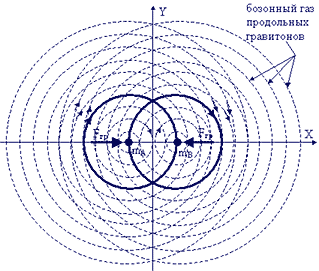
С точки зрения статистической физики полная энергия (кинетическая +потенциальная) гравитонного газа сохраняется, однако в гравитационном поле по отдельности не сохраняются энергия и импульс, импульс и момент импульса, момент импульса и энергия [11]. В области либрации АВ фиг.21 движение гравитонов по орбитам противонаправлено, а вне этой области за телами сонаправлено, что показано на фиг.22.

Фиг. 22 - схема процесса гравитации в модели согласованных и несогласованных вихревых движений гравитонного газа. Увеличить >>>

Для противонаправленных вихрей гравитонов в области АВ относительная кинетическая энергия возрастает, тогда потенциальная энергия вихрей уменьшается. Вне области либрации кинетическая энергия относительного движения вихрей уменьшается, а потенциальная — увеличивается, то есть возрастает давление гравитонного газа, создавая разность давлений или гравитацию. Указанное возрастание относительной подвижности квадрупольных деформаций вакуума газа гравитонов в области либрации АВ объясняется тем, что пространство здесь становится локально плоским, его группа Ли симметрии расширяется до всей группы афинных преобразований (сжатия-растяжение, крутильных и квадрупольных сдвигов, 3-х мерных вращений). Вне этой области группа Ли симметрии гравитационного поля сужается до подгруппы этой афинной группы в виде подгруппы вращения вокруг оси X. Данный факт установлен из анализа групповой симметрии системы уравнений Дирака-Максвелла в [12] или анализа симметрии классических уравнений Ньютона в [13]. Такое расширение группы Ли симметрии поля означает появление дополнительных степеней свободы движений у этого поля. По этим новым степеням свободы совершаются колебательные движения гравитационного поля, следовательно, возрастает кинетическая энергия этих степеней свободы, но тогда уменьшается потенциальная энергия, то есть уменьшается давление гравитонного газа в области либрации или давление квадрупольных деформаций вакуума. Возникает разность давлений или гравитация. Данный подход к объяснению гравитации, а, значит, гравилевитации с групповой (топологической) точки зрения является наиболее общим, и использовался для создания технических устройств, реализующих гравилевитацию.

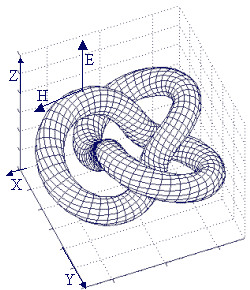
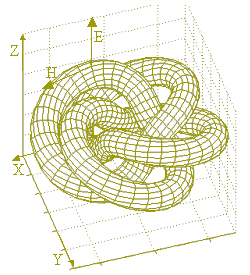
В результате краткого качественного описания принципа гравитации и гравилевитации, приведённого выше, можно сказать следующее. Анализ групповой симметрии нелинейных связанных уравнений Максвелла-Дирака проведённый в [12] позволил описать электромагнитные солитоны вакуума как физическую сущность в виде трёх топологически связанных полей: электромагнитного поля Максвелла (спина 1) в форме крутильного сдвига упругого вакуума, гравитационного поля Ньютона-Эйнштейна (спина 2) в форме квадрапольного сдвига (чистого сдвига) упругого вакуума, нейтринного поля Дирака (спина 1/2) в форме винтовых деформаций этого вакуума. ЭМ-солитон (спина 3/2) в форме торического узла трилистника или четырёхлистника проявляет свойства суперсимметричной частицы, обладающей объединёнными свойствами симметрии всех трёх полей в зависимости от условий возбуждения солитона и взаимодействия его с веществом. Качественный вид такого торического узла вихревой трубки спиральной деформации вакуума в форме трилистника и четырёхлистника показан на фиг. 23. Для сравнения там же показана примитивная (не заузленная) петля кванта электромагнитного поля в форме тора.

Фиг. 23 - сравнительные конфигурации торических вихрей деформаций вакуума для фотона и ЭМ-солитона. Увеличить >>>

Спины указанных узлов обусловлены внутренним движением спирали деформации по поверхности торов. Следует отметить, что гипотеза почти абсолютно жёсткого вакуума с объёмной жёсткостью в энергетическом исчислении 1/G~1-¹¹² эрг/см³ высказывалась ещё Декартом, затем Френелем для объяснения прозрачности вакуума в 1812 году. Вихри деформаций эфиро-вакуума рассматривались Максвеллом [6] для механической модели электромагнитного поля, а затем вихревой модели атомов. Позднее Кельвин и Тэт [14] предложили рассматривать узлы вихрей деформаций вакуума как модели электрона, а затем Тэт [24] начал классифицировать узлы по топологическим инвариантам. Дирак предложил рассматривать жёсткость вакуума как результат плотной упаковки частиц-античастиц в резервуаре Вселенной. Сахаров в работе [15] рассматривал иерархическое (доменное) устройство сверхжёсткого вакуума и работы эти продолжаются [16].В настоящее время для классического электромагнитного поля Максвелла получены многочисленные нетривиальные топологические решения в торических узлах электрического и магнитного поля в вакууме [17] и плазме [18], объясняющие устойчивые состояния шаровых молний. Известно [19] численное решение нелинейного поля Янга-Миллса (обобщение системы уравнений Дирака-Максвелла) в виде торического узла квазиэлектрического и квазимагнитного поля. Приведено [20] множество различных решений уравнений элементарных частиц в виде солитонов как многосвязанных торических гиперповерхностей многих размерностей, объясняющих с единой точки зрения существование различных взаимодействий: электромагнитных, гравитационных, ядерных и слабых (нейтринных). Перечень этих работ говорит о достаточной ординарности точки зрения на вакуум как специфическую многомерную среду, имеющую нетривиальные топологические характеристики.

Используя описанные выше представления, были созданы генераторы ЭМ-солитонов вакуума, которые, в зависимости от симметрии элемента антенны, генерировали торические трилистники или четырёхлистники [21]. С помощью этих антенн была доказана возможность гравилевитации.

ЛИТЕРАТУРА

1. Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. МоскваЧ Ижевск, R&C Dynamics, 2001
   
2. Тодд Р. и др. Солитоны и нелинейные волновые уравнения. М.:, Мир, 1988
   
3. Смелов М.В. Электромагнитные солитоны вакуума. Часть 1. Расслоенное пространство электромагнитных солитонов. Физическая Мысль России. М.:, МГУ, № 1/2, 1999, с. 61
   
4. Смелов М.В. Электромагнитные солитоны вакуума. Часть 3. Физические параметры электромагнитных солитонов. Физическая Мысль России. М.:, МГУ, № 3, 2000, с.62
   
5. Ланда П.С. Нелинейные колебания и волны. М.:, Наука, Физматлит, 1997
   
6. Прасолов В.В., Сосинский А.Б. Узлы, зацепления, косы и трёхмерные многообразия. М.:, МЦНМО, 1997
   
7. Ландау Л.Д., Лифшиц Е.М. Теория поля. М.:, Наука, 1967
   
8. Елисеев В.И. Введение в методы теории функций пространственного комплексного переменного. М.:, НИАТ, 1990
   
9. A.F. Ranada, J.L. Trueba. Electromagnetic knots. Physics Letters. A 202. 3, July, 1995, p. 337
   
10. Сахаров А.Д. Вакуумные квантовые флуктуации в искривлённом пространстве-времени. ДАН, СССР, т. 177, № 1, 1967
    
11. Коноплёва Н.П., Попов. В.Н. Калибровочные поля. М.:, Атомиздат, 1972
    
12. Смелов М.В. Электромагнитные солитоны вакуума. Часть 2. Топологические характеристики электромагнитных солитонов (продолжение). Физическая Мысль России. М.:, МГУ, № 2, 2000, с. 50
    
13. Беркович Л.М. Факторизация и преобразование дифференциальных уравнений. М.:, R&C Dynamics, 2002
    
14. Атья М. Геометрия и физика узлов. М.:, Мир, 1995
    
15. Сахаров А.Д. Существует ли элементарная длина. Физика в школе. М.: Квант, № 2, 1968, с. 6
    
16. Труды IX Международного семинара «Гравитационная энергия и гравитационные волны». Дубна, ОИЯИ, 1998
    
17. A.F. Ranada. Topological electromagnetism. J. Phys. A: Math. Gen. 25 (1992), p. 1621
    
18. A.F. Ranada, M. Soler, J.L. Trueba. Ball lighting as a force-free magnetic knot. Phys. Rev. E, v. 62, № 5, 2000, p.7181
    
19. L. Faddeev, A.J. Niemi. Knots and particles. http://www.arXiv: hep-th/ 9610193 v1 24 Oct 1996
    
20. Рубаков Ю.Л., Санюк В.И. Многомерные солитоны. М.:, из-во РУДН, 2001
    
21. Смелов М.В. Электромагнитные солитоны вакуума в 4-х частях. 4 Международная научно-техническая конференция (4МНТК) «Антенно-фидерные устройства, системы и средства радиосвязи» Сб. Трудов, Воронеж, 1999. - Воронеж: КБ АФУ, 1999. CD, RUS (ISBN5-84455-006-9). С. 425-494
    
22. Смелов М.В. Приёмопередатчик электромагнитных солитонов. Физическая Мысль России. М.:, МГУ, № 2, 1998, с. 31
    
23. Смелов М.В. Электромагнитные солитоны вакуума. Часть 4. Предварительные экспериментальные исследования, базирующиеся на модели электромагнитных солитонов. Физическая Мысль России. М.:, МГУ, № 1, 2001, с. 38
    
24. P.G. Tait. On knots I, II, III. Scientific Paperss Cambridge University, Press, 1900