Академия Тринитаризма -- Институт Ноосферного Естествознания -- Электронные публикации -- Комаров В М, Татур В Ю -- Принципы самоподобия и синхронности в музыкальной гармонии

АКАДЕМИЯ ТРИНИТАРИЗМА

Комаров В.М., Татур В.Ю.
Принципы самоподобия и синхронности в музыкальной гармонии

Oб авторе - Комаров В.М.

Oб авторе - Татур В.Ю.

Примерно в середине прошлого века в связи с развитием фрактальной геометрии [2,4,7,8,9,11-14] возникло понятие самоподобия, выражающее идею масштабно-пространственного подобия частей и целого, с безграничной экстраполяцией как во вне относительно некоторого избранного объекта, так и во внутрь. Фрактальное самоподобие – это новый инвариант подобия, не зависящий от масштаба рассмотрения явления.

В данной работе мы хотим показать, что идею фрактального самоподобия весьма уместно использовать для обоснования и более глубокого раскрытия понятия консонансности, относящегося к сфере звуковосприятия человека, чтобы в дальнейшем применять это понятие при моделировании и исследовании некоторых эффектов эмоциональной выразительности музыки. Как оказалось это можно сделать, используя понятие самоподобия не в пространственной, а во временной интерпретации, назвав его временным самоподобием (по аналогии с пространственным). Тем самым обобщается принцип самоподобия на временные явления.

Однако уместен вопрос: каковы основания для введения в рассмотрение принципа самоподобия применительно к временным явлениям?

Эти основания связаны с тем, что все виды изменений можно разбить на два больших класса: периодические и апериодические. Апериодически протекающие изменения являются незавершенными во времени процессами, их завершение предполагает бесконечное время. Циклическое же изменение воспроизводит себя за конечное время, поэтому у каждой циклически функционирующей системы период Т можно рассматривать как время самовоспроизведения и тем самым как время самоподобия, т.е. как некую фундаментальную характеристику ее динамики.

Из традиционно понимаемого определения периода циклического процесса, как времени между двумя любыми одинаковыми фазами изменения, происходящего внутри цикла, следует, что величина периода не зависит от точки привязки во времени (см. рис. 1). Период инвариантен к сдвигу фаз.

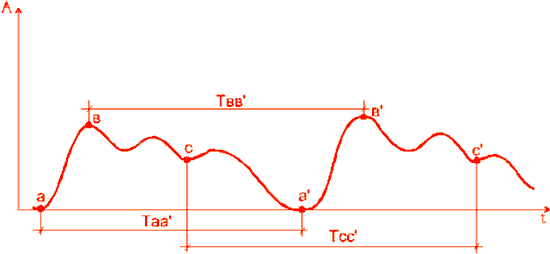
Т=Таа’=Твв’=Тсс’; f(t+Т)=f(t) и (0;Т)

Рис. 1. Определение периода колебания

При сложении двух процессов с одинаковыми периодами получаем результирующий процесс с тем же периодом, т.к., сдвигая фазу одного из процессов, их можно согласовать, совместить (см. рис.2). Аналогично можно получить и другое непосредственное следствие из определения периода: если время самоподобия кругового осциллятора Т_с, то добавление к нему нового процесса с временем самоподобия Т_с / 2 (удвоение частоты) не изменяет время самоподобия системы осцилляторов в целом (см. рис. 2.).

В процессе f₂(t) (рис. 3) присутствует период Т_с1=2Т_с2, поэтому суммирование процессов времени самоподобия не изменяется.

t- рассогласование выбранных фаз

t=0: рассогласование устраняется переносом начальной точки отсчета фазы первого процесса

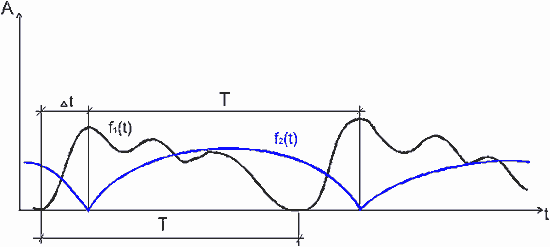
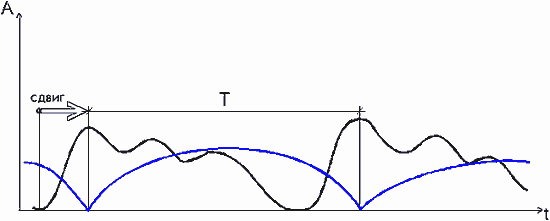
Рис. 2. Суммирование после согласования фаз дает тот же период суммарного процесса

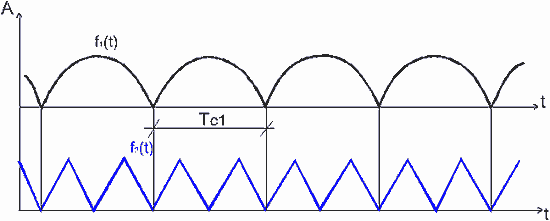
Рис. 3. Сложение процессов удвоенных частот

Напротив, добавление в систему вдвое меньшей частоты увеличивает период самоподобия вдвое. Этот случай является также достаточно очевидным следствием из определения периода колебания.

Что будет происходить с Т_с всего ансамбля при линейном наращивании величин частот, объединяемых в единый ансамбль?

Пусть исходная частота f₀. Все остальные получим умножением на коэффициент, кратный числам натурального ряда:

1(f₀); 2(f₀); 3(f₀)...; i(f₀)...

Нетрудно показать, что при совместном звучании частоты f₀ и одной из частот f₁, (значения которой кратны числам натурального ряда), период самоподобия такого ансамбля в целом также будет оставаться постоянным, равным f₀:

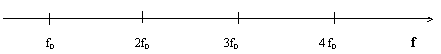
Значения частот добавляемых в целостный ансамбль, при исходной f₀

Тогда возникает вопрос: какие частоты при слиянии в ансамбль увеличивают его время самоподобия?

Покажем, что

удваивает время самоподобия колебательной системы осцилляторов добавление к ней осциллятора с частотой 3/2 от основной.

Пусть основной период системы Т_с. Тогда период добавленного осциллятора будет 2/3 Т_с. Выразим оба периода Т₁ и Т₂ через кратное значение Т_с /3:

Т₁=3/3 Т_с; Т₂=2/3 Т_с.

Встреча в фазе для этих осцилляторов будет происходить через время равное наименьшему общему кратному (НОК) чисел 3 и 2, т.к.

Т₁=3(Т_с /3); Т₂=2(Т_с /3).

Т.к. НОК(2,3)=6, то новый период Т_сn будет равен Т_сn=6(Т_с /3)= 2 Т_с.

В общем случае, если Т₁= Т_с и Т₂=n/m Т_с; mО {n+1;2n-1}, то время самоподобия системы из двух осцилляторов увеличится в n раз (формально Т_с оказывается увеличенным в n раз больше числителя дроби при Т₂=n/m Т_с.

В самом деле, пусть Т₁=m/m Т_с; Т₂=n/m Т_с, тогда Т₁=m(Т_с /m); Т₂=n(Т_с /m). Т.к. m и n не имеют делителей, то их НОК=mn. Следовательно, совпадение в одной фазе будет происходить за время Т_с_n=m n (Т_с /m)= n Т_с.

Пусть i изменяется так, чтобы Т₂ убывал в пределах от Т₂ до Т₂/2:

Т₂=n/(n+i)Т_с т.е. iО {1; n-1}.

Тогда всех случаи, когда n и n+i не имеют простых общих делителей, сводятся к предыдущему. Если же n и n+i имеют общий делитель p, то после сокращения (n/p)/((n+i)/p)=n'/m', получаем, что время самоподобия (числитель дроби) уменьшается в p раз, а сам этот случай вырождается в случай более высокого порядка самоподобия (т.е. при меньшем времени).

Результаты парного синтеза частот приведены в таблице 1 (отношения частот выражены в рациональных числах). Для примера рассмотрим третью строку этой таблицы. В третьей строке приведены значения частот, выраженных в виде рациональных чисел:

5/4; 3/2; 7/4.

При парном сложении с основной частотой они учетверяют ее время самоподобия. Причем случай с частотой 6/4=3/2 и ему подобные являются вырожденными (происходит удвоение времени самоподобия — случай квинты), поэтому в таблице они специально выделены. С помощью некоторых частот (табл.1) можно провести приближенную численную запись значений частот темперированного ряда Царлино-Веркмайстера-Нейдгрдта [1,3,5,6,10]. Как известно частоты музыкального звукоряда строятся в геометрической прогрессии от исходной со знаменателем 2^1/12:

, , .

Рациональные выражения значений частот разбиения октавы Таблица 1

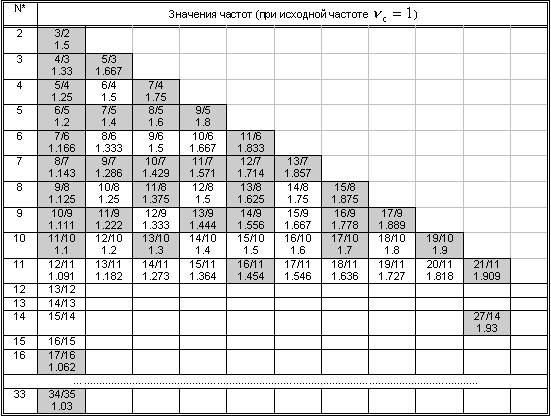
N – кратность увеличения Т_с.

Значение частоты f(i) ноты 12-ступенного ряда в зависимости от номера ступени i можно выразить по формуле:

f(i)=2 ^{i /12}.

Значения частот музыкальных звукорядов, и их приближение рациональными числами, а также погрешности этих приближений приведены в табл.2. В отношении времени самоподобия парных комбинаций указанных частот с основной все частоты могут быть строго упорядочены, причем, эта упорядоченность в связи с нарастанием времени самоподобия усиливает в субъективном их восприятии человеком ощущение диссонансности.

Элементарные системы темперации S=12 и S=24. Таблица 2

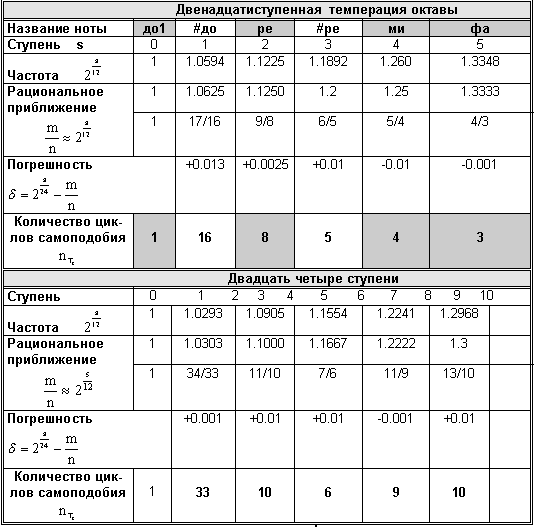
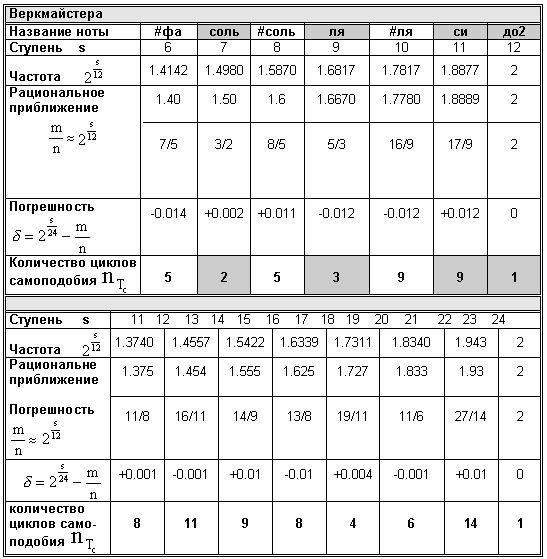
Сравнение значений частот представленных в рациональном приближении (таблица 1) со значениями частот темперированной октавы (по Царлино-Веркмайстеру-Нейдгардту, см. таблицу 2) позволяют, сопоставляя со значениями частот равным 2^1/12 (при суммировании с основной), определить кратность увеличения времени самоподобия системы.

Ряд частот строится как геометрическая прогрессия:

q_c=2^1/12 (темперация Царлино-Веркмайстера-Нейдгардта);
q_d=2^1/24 (темперация в 24 ступени (Нейдгардта-Араамова-Римского-Корсакова)).

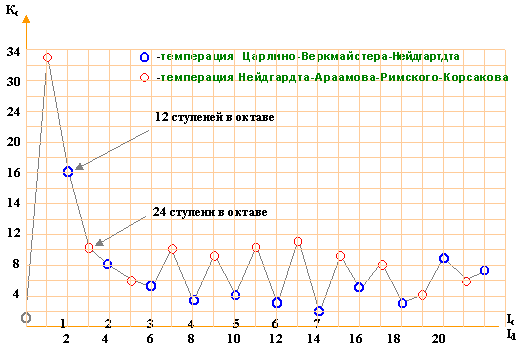
Количественная оценка других видов темперированных шкал в пределах логарифмического деления звуковой шкалы от 5 до 27 приведены на рис.4, а сравнительные данные по критерию времени самоподобия в таблице 2.

К_с - степень увеличения Тс времени самоподобия; I_n - номер ступени по Царлино-Веркмайстера-Нейдгрдту;

Рис. 4. Зависимость увеличения степени времени самоподобия (К_с) совместного звучания двух звуков до1 и звуков ступеней I_nили I_d систем темпераций с S=12 и S=24.

Из таблицы 3 видно, что двузвучия разбиваются на две группы: одна – консонантно звучащих, другая – диссонантно. Причем, сочетание до₁-до₂ дают октавное слияние звучания – максимальный консонанс, сочетание до₁-соль есть квинтовый интервал, является основой доминантного трезвучия. Звучание квартовое до₁-фа является основой субдоминантного трезвучия, а до₁-ля – основа «параллельного» минора. Аккорд до-ми-соль является основным, максимально устойчивым звукообразованием и имеет название «тоническое трезвучие». Таким образом, все консонансные сочетания являются основой музыкальной гармонии и прямо связаны со временем самоподобия совместного звучания.

Таблица 3

растет ¬ консонанс ® убывает

Т_с	1	2	3	4	5	8	9	16
совместно звучащие ноты	до₁-до₂	до₁-соль	до_1-фа до₁-ля	до₁-ми	до₁-ре# до₁-фа# до₁-соль#	до₁-ре	до₁-ля# до₁-си	до-до#
консонансные сочетания				диссонансные сочетания

Анализ результатов, полученных с использованием принципа самоподобия, позволил сделать следующие выводы:

Согласованность изменений во времени различных периодических процессов, соединенных в единое целое возможно количественно оценивать на основе принципа самоподобия;
Субъективное ощущение степени консонасности также объективно оценивается временем самоподобия ансамбля;
Мажорные и минорные, как ансамбли, отличаются по времени самоподобия в 2,5 раза;
Темперация Царлино-Веркмайстера-Нейдгардта – наилучшее начальное и при этом еще и достаточно полное средство выражения идей согласия динамических частей в единое целое;

Историческая справка по элементарным системам темпераций [5,6].

Количество ступеней в октаве S	Кем открыта или реализована система темперации
12	А. Веркмайстер (1645-1706) Расчет и реализация. И.С. Бах ( 1685-1750) в 1722 г создал в этой системе целый ряд произведений, продемонстрировав ее возможности.
17	Древняя система арабов. Известна ранее 10в. до РХ. Неравномерно темперирована. А.С. Оголевец (1941) Использовал эту систему в теоретико-музыкальных построениях.
19	Итальянская система эпохи возрождения. Д. Царлино (1517-1590) Л. Фольяни ( -1539) М. Преториус (1619)
20	Г.Б. Дони (1635)
21	П. Барановский , Е. Юцевич (1956)
22	Древняя индийская система «Шрути». Неравномерно темперирована
24	Н.Г. Нейдгарт (1718) А. Араамов , Г. Римский-Корсаков ( 1920 г) J. Dinnan и др.USA патент EP 0 436 976 A1.(1989) Версия 22 ступенной равномерной темперации.
26	М. Мерсен (1636)

Литература

Авдеев Л.В., Иванов П.Б. Математическая модель восприятия звукорядов. -Дубна: 1990.
Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. -М.: Наука, 1990.
Музыка и математика (под ред. Г. фон Карояна). -М.: Наука, 1994.
Пайтген Х. О., Рихтер Л. Х. Красота фракталов. – М.: 1993.
Риман Г. Акустика с точки зрения музыкальной науки. -М.: 1898.
Риман Г. Катехизис истории музыки. -М.: 1896-97.
Трахтенброт Б.А., Турбин А.Ф., Працевитный Н.В. Фрактальные множества, функции, распределения. -Киев, 1992.
Федер Е. Фракталы. -М.: Мир, 1991.
Фракталы в физике. -М.: Мир, 1988.
Фрактальные объекты в математике, физике и биологии. Киев, 1991.
Mandelbrot B. The Fractal Geometry of Natyre — W.H. Freeman. 1983.
Mandelbrot B. Fractals and Multifractals: Noise, Turbulence and Galaxies. New York: Springer. 1988.
Mandelbrot B. The Fractal Geometry of Nature. Revised Ed., San Francisco: Freeman W.H. 1982.
Mandelbrot B. Fractals: Form, chance and dimension.1977.

Комаров В.М., Татур В.Ю. Принципы самоподобия и синхронности в музыкальной гармонии // «Академия Тринитаризма», М., Эл № 77-6567, публ.11019, 19.02.2004

[Обсуждение на форуме «ИНЕ»]