ПРОБЛЕМА ЗАДАЧИ «КВАДРАТУРЫ КРУГА» (Построить, с помощью циркуля и линейки без делений, квадрат равновеликий данному кругу) по мнению историков, существовала уже за две тысячи лет до н.э. Свидетельства о первых решениях датируются V веком до н.э. По свидетельству древнегреческого историка Плутарха, философ Анаксагор, коротая время в тюрьме, пытался построить квадрат равновеликий очерченному кругу.

Задача квадратуры круга возникла, прежде всего, из практических проблем общества. Уже в глубокой древности философы заметили, что мир устроен по принципу кругового вращения. То есть изначльной мерой бытия всего сущего является круг. Человечество же мерой своего практического бытия и творения избрало квадрат. Так возникла проблемная задача приведения в соответствие круговых и квадратных мер бытия. Решая эту задачу, древние пытались земное бытие и творение общества гармонизировать с небесным (космическим) бытием и творением, исходя в основном из духовных (религиозных) побуждений. В настоящее время актуализация древнейшей задачи обусловлена не только духовными, но и практическими проблемами гармонизации земного и космического бытия и творения общества.

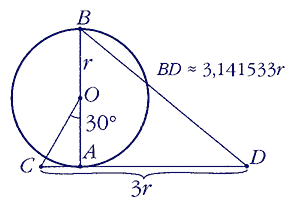
За историю цивилизации было предложено множество построений, в том числе и автором данной публикации, которые давали приближенное решение задачи. И, хотя задача решается уже тысячи лет, но путаница в истинности смысла ее решения продолжается до наших дней. Яркий образец подобных путаниц помещен в «Энциклопедии для детей». Рассмотрим помещенный там рисунок, который по заверению Владимира Дубровского «дает приближенное значение π с достаточно хорошей точностью» [2].

В согласии с рисунком, и произведенными по нему вычислениями, АС ≈ 0,5774r; АD ≈ 2,4226r; BD ≈ 3,141533r. Но это не есть значение π, поскольку оно выражено в мерах радиуса данного круга. Любому школьнику известно, что π – длина окружности данного круга ≈ 6,2831852r или ≈ 3,1415926d.

Данное решение ни как не согласуется с утверждением: «Если радиус данного круга равен r, то сторона равновеликого этому кругу квадрата равна х. Таким образом, надо построить отрезок , т.е. r графически умножить на ». [3]

Даже на глаз видно, что построенный прямоугольный треугольник ABD не равен по площади данного круга. А если точно, то его площадь ≈ 0,5 х 2,4226r x 2r ≈ 2,4226r². Если прибавить площадь треугольника АСО ≈ 0,2887r², тогда получим такой вот ломанный, разносторонний 4-х угольник BDCO, площадь которого ≈ 2,7113r² < πr². Без сомнения можно сказать, что – это один из множества самых не точных и неудачных вариантов решения задачи «квадратуры» круга.

ОДИН ИЗ САМЫХ «ТОЧНЫХ» ВАРИАНТОВ РЕШЕНИЯ ЗАДАЧИ «КВАДРАТУРЫ» КРУГА.

В качестве исторической справки, должен упомянуть, что мерой моего первого варианта решения задачи было «вещественное число», т.е. 0,5r [4]. Задача была решена с точностью π ≈ √3,14644r² (0,15%.). Это была самая высокая точность после решения Гюйгенса (0,238%) и при этом с меньшим количеством затраченных операций на построение. Второй вариант решения задачи был осуществлен мерой «золотого сечения» (мерой 0,6180339r) в 2003 г. [5]. Полученный результат π ≈ √3,14530r² (точность 0,095%.). Однако операций построения на него затрачено несколько больше.

Вариант 3. [6] В предыдущих своих вариантах решения задачи я исходил из того, что фундаментальным началом (основанием) для построения равновеликого квадрата данному кругу является одна из хорд данного круга, а точнее, является один из множества, вписанных прямоугольных треугольников в данный круг. Ниже предлагаемый вариант решения задачи осуществлен на тех же началах и с учетом подсказки Платона:

«Итак, нам приходится отдать предпочтение двум треугольникам, как таким, из которых составлено тело огня и (трех) прочих тел: один из них равнобедренный, а другой таков, что в нем квадрат большей стороны в три раза больше квадрата меньшей». [1]

Данный вариант – вариант синтетического решения «задачи квадратуры круга», в согласии с линейным «законом движения вещественного числа» — (0,5)⁰ = (0,5)ⁿ + (0,5)ⁿ + (0,5)^n-1 + … + (0,5)³ + (0,5)² + (0,5)¹ и «циклическим законом превращения равнобедренного треугольника в равносторонний» — (С1 – О1® О2® С2 – О2® О3® С3 – О3® С4 – О4® О5® С5 – О5® …).

Произведем последовательное построение квадрата равновеликого данному кругу О (Рис. 2):

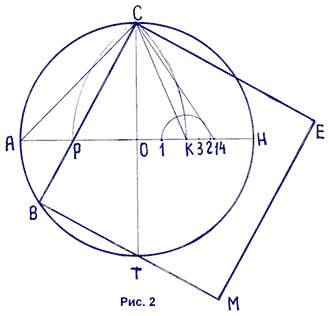
1. Радиусом r =1 в точке О чертим окружность.
2. Проводим через точку О два взаимно перпендикулярных диаметра СТ и АН.
3. Соединяем прямой точки А и С. АС – сторона вписанного в данный круг квадрата.
4. Ставим ножку циркуля в точку А и радиусом АС чертим дугу до пересечения ее с диаметром АН в точке К.
5. Соединяем прямой точки С и К. СК – гипотенуза прямоугольного ∆СОК, а ОК – проекция СК на ОН = r.
6. Отрезок ОК делим пополам и отмечаем точкой 1.
7. Ставим ножку циркуля в точку К и переносим круговым движением отрезок К1 в точку 2 и получаем отрезок О2 (сумму отрезков: ОК + К1), удлинив таким способом отрезок ОК на половину его длины.
8. Отрезок К2 делим пополам в точке 3 и получаем отрезок 3 – 2. Далее аналогичным способом продолжаем деление половинных отрезков до 14 деления включительно. Посредством циркуля последовательно суммируем отрезок ОК и половинные отрезки, обозначив их порядковыми номерами половинного деления: 1, 3, 5, 6, 8, 9, 11, 14. В конечном итоге мы получаем отрезок О14.
9. Точку С соединяем прямой с точкой 14 на отрезке ОН.
10. Ставим ножку циркуля в точку 14 и круговым движением отрезка 14С чертим линию до пересечения ее с радиусом круга ОА в точке Р.
11. С точки С, через точку Р, проводим прямую линию до пересечения ее с периметром данного круга в точке В.
12. Хорда ВС – сторона квадрата равновеликого данному кругу. А прямоугольный треугольник СВТ – фундаментальное основание для построения квадрата равновеликого данному кругу.
13. Строим квадрат СЕМВ, равновеликий данному кругу.

Доказательство:

Все доказательство утверждения п. 12 сводится к вычислению площади построенного квадрата или длины отрезка ВС. Равенство площадей равновеликого квадрата данному кругу выражается уравнением: (ВС)² = πr², где π ≈ 3,1415926; ВС . Таким образом, необходимо доказать, что ВС =

АК = АС – по построению. АК =

ОК = АК – ОА; ОК = 1,4142135r – r; ОК ≈ 0,4142135r.

При последовательном делении отрезка ОК и каждой последующей его части на две равные части мы получим следующие числовые значения отрезков:

К отрезку 0,4142135r приплюсуем все подчеркнутые числовые значения отрезков и в итоге получим длину отрезка О14 ≈ 0,6951673r.

Рассмотрим прямоугольный ∆ОС14. (С14)² = (ОС)² + (О14)².

Подставив в буквенные их числовые значения вычислим:

С14 = . ОР = 1,2178905r — 0,6951673r ≈ 0,5227232r.

∆РОС – прямоугольный. В согласии с теоремой Пифагора:

(СР)² = (ОС)² + (ОР)²; СР =

∆РОС и ∆СВТ – прямоугольные и углы у них равны. Следовательно, стороны находящиеся против равных углов – пропорциональны:

ОР : ВТ = СР : СТ; ВТ = (ОР Ч СТ) : СР. Подставим вместо буквенных обозначений их числовые значения:

ВТ = (0,5227232r Ч 2r) : 1,1283791r ≈ 0,9265028r.

∆СВТ – прямоугольный. (ВС)² = (СТ)² – (ВТ)². Подставим в данное уравнение вместо буквенных обозначений их числовые значения:

(ВС)² = (2r)² – (0,9265028r)²;

BC =

Таким образом, ВС . Что и требовалось доказать.

Отметим при этом:

1. Построенный квадрат, равновеликий данному кругу, относительно системы координат повернут на значительный угол.

2. Построенный ∆СО14 ~ соответствует параметрам треугольника, указанным Платоном: (С14)² : (О14)² ≈ 3. Подставив числовые значения С14 и О14, убедимся в верности нашего утверждения:

(1,2178905r)² : (0,6951673r)² ≈ 1,4832572r : 0,4832575r ≈ 3,0692895.

3. В отношениях сторон рассматриваемых треугольников, примерно такое же соотношение сторон «золотого» треугольника, стороны которого соответственно равны: r; 1,1755705r и 0,6180339r.

1,1755705r : (0,6180339r)² ≈ 1,1755705r : 0,3819659r² ≈ 3,0776844r ^-1. Возможно, в этом совпадении неравнозначных отношений сторон до третьего знака после запятой существует какой-то сакральный смысл. Здесь существует некая аналогия с приближенным равенством отношений длины периметра круга к его диаметру и площади круга к квадрату его радиуса. Об этом – в следующей «Беседе».

Другие варианты решения задачи «квадратуры» круга автором будут представлены в следующей «Беседе».

ЛИТЕРАТУРА:

1. Платон. Собр. соч. в 4-х т. «Мысль», М., 1994. Т.3, с. 457-458.
2. Энциклопедия для детей. Том 11, математика, М., «Аванта+»,1998, с.323
3. Математический энциклопедический словарь. М., 1988. С.264.
4. Сергиенко П.Я. Триалектика. Задача квадратуры круга и ее решение. 22с. Пущино – 1997.
5. Сергиенко П.Я. Рецензии и отзывы на решение задачи. Построение квадрата равновеликого кругу мерой «золотого сечения» круга. «Академия Тринитаризма», М., Эл № 77-6567, публ. 07.04.2003.
6. Сергиенко П.Я. Начала. Триалектика сакральной геометрии. 32с. Пущино – 2005. С.20 – 23.