|
|
Сергиенко П.Я.
Развитие принципов и аксиом синтетической геометрии триалектики
Поступили первые отзывы, замечания и вопросы на публикацию тезисного изложения логико-аксиоматических начал «синтетической геометрии триалектики» (С Г Т). Благодарю всех, отозвавшихся. Заранее благодарю всех, кто пришлет, в адрес E-mail: ssp@online.stack.net Сергиенко Петру Якубовичу или E-mail: info@trinitas.ru «Академия Тринитаризма», свои статьи, развивающие С Г Т, для опубликования.
Из первых отзывов следует, что только у профессора В.С.Воронина не возникло недоразумений к утверждению:
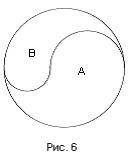
««Золотое» сечение круга на части «А» и «В», аналогичное «золотому» сечению отрезка, производится континумой, радиусами которой будут соответственно R1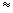
0,618033988945r и R2 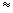0,381966r, где r – радиус данного круга, делимого в отношении «золотого» сечения. То есть, если площадь данного круга равна 1, то площадь его частей: А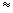0,618; В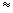0,382.
Таким образом, в данной геометрической форме (Рис. 6) «золотого» сечения круга мы имеем очевидное проявление триединства континуумного синтеза мер: «золотого» сечения радиуса круга; «золотого» сечения континумы и «золотого» сечения круга».
В этой связи «очевидности» недостаточно и требуется доказательство теорем:
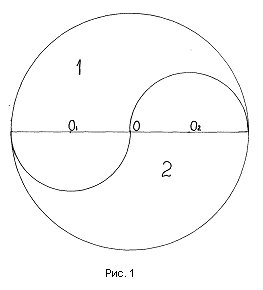
Теорема 1: При делении круга континумой на две части, площадь любой части круга равна произведению значений трех величин – числа «пи», радиуса круга (r) и радиуса континумы (rn).
Для доказательства теоремы рассмотрим два рисунка. На Рис.1 континума, делящая круг на две равные части, проходит через центр круга. О1О – радиус (r1) части 1 (континуумы 1). ОО2 – радиус (r2) части 2 (континуумы 2) где r1 = r2 = 0,5r. О1О2 = r1 + r2 = r. (1).
Площадь круга S=S1 + S2 = πr2
(2).
Подставляя значения (1) в формулу (2) в конечном итоге мы получим: S1 = πr r1; S2 = πr r2. (3).
Из формулы (3) вытекает следствие:
Площади континуумы 1 и континуумы 2 относятся между собой как радиусы их континум.
S1: S2 = r1: r2. (4)
То есть континуумные площади частей круга относятся между собой не так как относятся площади одного круга к другому (как квадраты их радиусов), а относятся как линейные отрезки.
Утверждения (1), (2), (3), (4) правомерны так же к Рис.2, где континума делит площадь круга на произвольные две части, поскольку всегда сохраняется равенство r1 + r2 = r.
Если круг делится на множество разных по площади континуумных частей, утверждения (1), (2), (3), (4) так же остаются в силе.
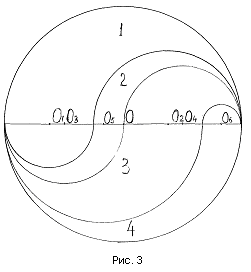
Теорема 2: Площадь любой внутренней континуумы, находящейся в средине круга, всегда равна разности крайних континумных площадей, подобных площадям 1 и 2.
Рассмотрим Рис. 3, где О1; О2; О3; О4; О5; О6 – центры диаметров континуумных площадей, радиусы которых соответственно равны: r1; r2; r3; r4; r5; r6. При этом r3 = r4 = 0,5 r; r1 + r2 = r ; r3 + r4 = r ; r5 + r6 = r. Соответственно континуальные площади будут вычисляться по формулам: S1 = πr r1; S4 = πr r4; S1+2 = πr r3; S3+4 = πr r6.
Промежуточная площадь, например, площадь континуумы 3 будет вычисляться по формуле: S3 = S3+4 — S4.
Сергиенко П.Я. Развитие принципов и аксиом синтетической геометрии триалектики // «Академия Тринитаризма», М.,Эл № 77-6567, публ.10983, 05.02.2004
[Обсуждение на форуме «Наука»]
Развитие принципов и аксиом синтетической геометрии триалектики
0,618033988945r и R2 0,381966r, где r – радиус данного круга, делимого в отношении «золотого» сечения. То есть, если площадь данного круга равна 1, то площадь его частей: А0,618; В0,382.
(2). |
Сергиенко П.Я. Развитие принципов и аксиом синтетической геометрии триалектики // «Академия Тринитаризма», М.,
 |