|
|
|
Jay Kappraff
of the Parthenon and its Meanings
University Heights
Newark, NJ 07102
E-Mail: Kappraff@aol.com
Abstract
Based on the PhD thesis of Anne Bulckens, the proportional system of the Parthenon is examined. With the appropriate choice of a module and the length of a «Parthenon foot», all dimensions are shown to be integers. These integer values are shown to be related to the musical scale of Pythagoras. Among the many musical relationships expressed by this structure, this paper focuses on a pentatonic scale made up of lengths, widths and heights of the outer temple and the inner temple or cella.
The Parthenon, dedicated to Athena Parthenos, is one of the most measured buildings that has survived antiquity. It was constructed between 447-438 B.C., which
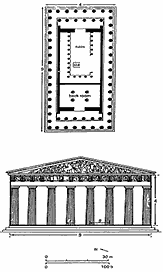
places it between the ages of Pythagoras (570-497 B.C.) and Plato (428-347 B.C.). It has been shown by scholars to have been built with extraordinary precision. It is a Doric temple with some Ionic features. There are eight columns along the East and West facades and 17 columns to the North and South (see Figure 1). The outer temple is adorned by metopes depicting scenes from Greek mythology. Within the outer temple is an inner temple called the cella, consisting of two chambers: the naos housing the statue of Athena and the opisthodomos, which once served as the treasury for the Delian league (see Figure 2). The cella is ringed by a continuous frieze depicting the four yearly Panathenaic procession of ordinary Greek citizens. Though it is generally agreed that the temple’s overall proportions of width to length and height to width follow the ratio 4:9 (see Figure 2), no one has adequately determined the temple’s underlying proportional scheme and its meaning, which was the raison d’être for such precise measurements.
Anne Bulckens has addressed these questions, in her recent Ph.D thesis from Deakin University in Geelong, Australia [1,2,3], by her discovery of a single module of length 857.6 mm., the average width of a «theoretical triglyph», following the writings of Vitruvius’ who stated that «Within a temple a certain part should be selected as a standard …the size of the module for Doric temples should equal the width of a triglyph». The width of this Parthenon module is equal to the width of a «theoretical triglyph», which was the width of a triglyph in the first design stage of the Parthenon before the frieze became shorter than the stylobate. This measure of a module agreed well with the result of a computer analysis carried out in 1984 by the scholar, Ernst Berger, in which 858 mm was found to occur most frequently as a common denominator of the length, width, and height measurements. Bulckens then discovered that when this module is divided by 2.5 to obtain a Parthenon foot of length 343.04 mm, and when this foot is subdivided into 16 equal parts, as was the convention of the time, referred to as «Dactyls» (D), all of the main measurements of the Parthenon can be represented as integers. (The use of the dactyl as main measuring unit might have started with the Great Temple of Apollo at Delos, begun 460 B. C.). This measurement of a foot is larger than the common Greek foot measurement of 293-295 mm. Bulckens has also drawn on the history and mythology of the Parthenon and the mathematics and numerology of Pythagoras. It will be explained here, why this structure can be regarded as one of the finest examples of Pythagorean theory at work.
With the help of the mathematician-musician Kappraff and the ethnomusicologist Ernest McClain, Bulckens has been able to show that all the key measurements are related to the ancient musical scale of Pythagoras, and this temple can be said to be an example of musically inspired architecture. The fundamentals of the ancient musical scale can be found in references [1,3,4,5]. Although the ratio of 9:4 is the proportion that is most visible within the Parthenon, the ratio of 3:2, the musical fifth, is in fact the key proportion used throughout the Parthenon. The ratios of length, width, and heights of the outer temple to the length, width and heights of the inner temple (cella) are all in the ratio of 3:2. It was Bulckens’ discovery that the geometric mean between 9 and 4 at 6 is essential to decoding the architectural motif of 9:6::6:4 as ruled by perfect fifths of 3:2. Both members of the tonal dissonance of 9:4, defining a musical ninth, are consonant with their geometric mean at 6). We found that the Renaissance architects Alberti and Palladio employed the musical proportions in a similar way [6]. Moreover, the width of the cella, which is the inner temple, measures 24 modules (960 D), which is the geometric mean of 16 modules (640 D) and 36 modules (1440 D) the column height plus the entablature and the width of the stylobate (the temple platform) respectively, resulting in the 9:6::6:4 proportion. Likewise, the length of the cella, 54 modules (2160 D), is the geometric mean of the outer temple’s stylobate width, 36 modules, and stylobate length, 81 modules (3240 D), again resulting in the 9:6::6:4 proportion. The fact that 6 is the mean proportional between 4 and 9 suggests that a rectangle of area 9x4 equals a square of area 6x6. Indeed Figures 3 and 4 show that the 9:4 proportion of the east façade has the same area (16x36 modules) as the square with side 6 (24x24 modules). In addition to serving as the width of the cella, 24 modules is the height of the temple from the stylobate to the top of the acroterium (a design in the center of the temple now gone). Several other examples can be found in the Parthenon also exhibiting the 9:6::6:4 proportion. Thus Kappraff found that the dimensions of the outer temple to the inner temple are determined by this proportion, and that in a sense, the inner temple of the Parthenon succeeds in rendering the entire temple into a consonant whole.
The dimensions of the inner and outer temples give rise to a succession of lengths corresponding to four successive musical fifths: 81:54:36:24:16 defining C:G:D:A:E as string lengths. (The black keys of the piano Fsharp, Gsharp, Gsharp, Dsharp, Asharp, or Bflat, Eflat, Aflat Dflat, Gflat, enjoy the same spacing.). In a «tone circle» these five arithmetical «modular residues» are unaffected by the «octave doubling» that allows them to define five different pentatonic modes, and they appear to the eye simply as an Egyptian 5-pointed «star glyph», viewed from various angles. The musical fifth enters in another way. For example in the naos, the statue of Athena was positioned at the ratio of 3:2 from the east stylobate edge.
It is well known that the Parthenon exhibits several prominent architectural ‘refinements’. For example, the stylobate (the main platform, upon which the columns of the peristyle rest) and frieze are slightly curved; the interaxials are not identical but have small variations; the columns are inclined inwards, etc. Bulckens has shown that, rather than being of merely aesthetic significance, the unique measurements of these refinements helped ensure that the design of the Parthenon was based on simple ratios (listed above) between the measurements of the key components of the Parthenon. Bulckens surmises plausibly from the evidence how the final design emerged in successive stages. The stylobate, for instance, probably was conceived as first sectioned into six 3:4:5 triangles. The curious design of the cella walls likely emerged from its earlier conception as paired triangles of 5:12:13, then cleverly sectioned into two rooms. Thus there are layers of geometrical implication not immediately visible to the eye.
Also noteworthy in this structure is the prevalence of dimensions commensurate with the numbers 60 and 10, reflecting the fact that both base 60 or sexagesimal system and base 10 systems were utilized by the Greeks as they were for the Babylonian and Sumerian Civilizations before them. For example, the metopes measure 60 Dactyls while the module is 40 Dactyls, with 60 and 40 constituting two important numbers from the sexagesimal system. The six 3,4,5-triangles covering the stylobate each have an area of 777,600 square Dactyls. This large number glorifies Athena the ‘Virgin’ (through the number 7), the base 60 system, and the powers of 10 alluding to a base 10 system and characterizing the Greek tetractys (a diagram of 10 stones that forms the basis of Pythagorean number theory, music and cosmology). Furthermore, the 5,12,13- triangle in the cella has a perimeter of 6000 Dactyls. These are a few of the many connections to Pythagorean number and number symbolism.
Bulckens has used the highly regarded measurements of Francis C. Penrose throughout her analysis and has set a criteria of error analysis in which errors no greater that 0.2% are tolerated. However, most measurements are much more precise, well below 0.1%. This gives her work a high degree of credibility. As a result, she has discredited the popular misconception that the proportions of the Parthenon are governed by the golden mean, since this hypothesis falls well outside of the error margin that she will tolerate. With contributions from Kappraff and McClain, her work tells the story of how this great building was a product of its age. The story involves history, mythology, architecture, mathematics, and musical theory, all reflecting on each other.
Acknowledgements by Bulckens
Since nine months, McClain and Kappraff have been so kind to contribute to my Parthenon research. With their strong backgrounds in musical theory, McClain and especially Kappraff provided me with a much better understanding of ancient music, making me realise how deeply the Parthenon design was rooted in Pythagorean music. By thoroughly examining my research, by asking the right questions, by pointing out errors, by eliminating suppositions that appeared too speculative, by providing explanations and background theory, I was able to find the Parthenon design issues in regard to music, while Kappraff also found some new Parthenon findings in this regard. I truly appreciate their contributions and insight.
References
1. A. Bulckens, «The Parthenon’s Main Design Proportion and its Meaning», PhD Thesis from Deakin School of Architecture, Geelong Australia. 2001.
2.A.Bulckens, «The Parthenon’s Symmetry» in Symmetry: Art and Science (Fifth Interdisciplinary Symmetry Congress and Exhibition of the ISIS-Symmetry), Sydney, July 8-14, 2001), no. 1-2, 38-41. 2001.
3. J. Kappraff, «Anne Bulckens’ System of Proportions of the Parthenon and its Meaning», A talk at the Carleton University School of Architecture in Ottawa, Canada. Also written as an article. In preparation (2002).
4. E.G. McClain, The Pythagorean Plato, York Beach, ME: Nicolas-Hays. 1978, 1984.
5. J. Kappraff, Beyond Measure: Essays in Nature, Myth, and Number, Singapore: World Scientific. 2002.
6. R. Wittkower, Architectural Principles in the Age of Humanism, First published in 1949 as Volume 19 of the Studies of the Warburg Institute, New York: John Wiley. 1998.
Illustrations

Figure 1: The Parthenon as seen from the northwest. From «Acropolis Restoration: The CCAM Interventions» by Manolis Korres, Academy Editions, London, 1994.
|
Figure 2: The cella consisting of the naos and the opisthodomos. Drawing by Susan Woodford. |
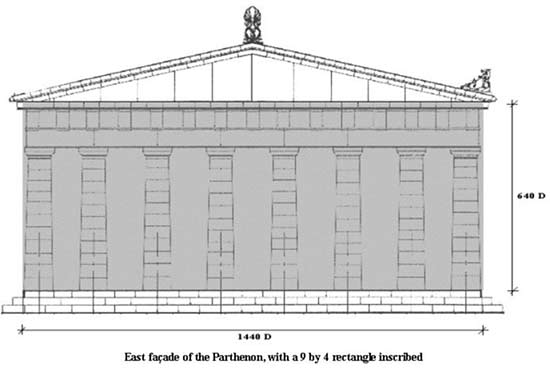
Figure 3: The East façade of the Parthenon darkened to show the ratio of 9:4 between width of the stylobate and height of column plus entablature.
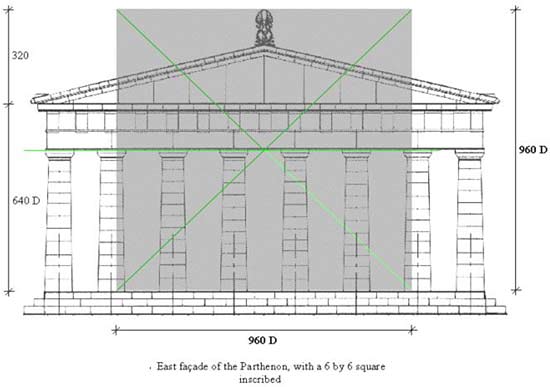
Figure 4: The East façade of the Parthenon showing a 6x6 square with the same area as the 9x4 rectangle. The width of the cella forms the width of the square while the height of the temple to the acroterium forms the height of the square.
Jay Kappraff, Anne Bulckens’ Analysis of the Proportions of the Parthenon and its Meanings // «Àêàäåìèÿ Òðèíèòàðèçìà», Ì.,
|
|